Phương pháp giải:

- Sử dụng công thức \({\sin ^2}x = 1 - {\cos ^2}x\), đưa hàm số về một ẩn \(\cos x\).

- Đặt \(t = \cos x\), tìm khoảng giá trị của \(t\). Đưa bài toán về ẩn \(t\).

- Cô lập \(m\), đưa bất phương trình về dạng \(m \ge f\left( t \right)\,\,\forall t \in \left[ {a;b} \right]\), khi đó: \(m \ge \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( t \right)\).

 - Lập BBT của hàm số \(y = f\left( t \right)\) trên đoạn đang xét và kết luận.

Lời giải chi tiết:

Xét hàm số\(y = {\cos ^3}x - 3{\sin ^2}x - m\cos x - 1\) trên \(\left[ {0;\dfrac{\pi }{2}} \right]\).

Ta có:

\(\begin{array}{l}y = {\cos ^3}x - 3{\sin ^2}x - m\cos x - 1\\y = {\cos ^3}x - 3\left( {1 - {{\cos }^2}x} \right) - m\cos x - 1\\y = {\cos ^3}x + 3{\cos ^2}x - m\cos x - 4\end{array}\)

Đặt \(t = \cos x\), với \(x \in \left[ {0;\dfrac{\pi }{2}} \right]\) thì hàm số \(t\left( x \right) = \cos x\) nghịch biến trên \(\left[ {0;\dfrac{\pi }{2}} \right]\) và \(t \in \left[ {0;1} \right]\).

Khi đó bài toán trở thành tìm\(m\) để hàm số \(y = {t^3} + 3{t^2} - mt - 4\) nghịch biến trên \(\left[ {0;1} \right]\).

\(\begin{array}{l} \Rightarrow y' = 3{t^2} + 6t - m \le 0\,\,\forall t \in \left[ {0;1} \right]\\ \Leftrightarrow m \ge 3{t^2} + 6t\,\,\,\forall t \in \left[ {0;1} \right]\,\,\,\,\left( 1 \right)\end{array}\)

Xét hàm số \(f\left( t \right) = 3{t^2} + 6t\) trên \(\left[ {0;1} \right]\) ta có: \(f'\left( t \right) = 6t + 6 = 0 \Leftrightarrow t =  - 1.\)

Bảng biến thiên:

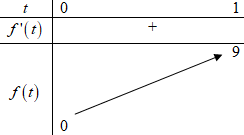
Dựa vào bảng biến thiên ta có bất đẳng thức (1) xảy ra \( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ {0;1} \right]} f\left( t \right) \Leftrightarrow m \ge 9.\).

Chọn C.