Câu hỏi
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình sau
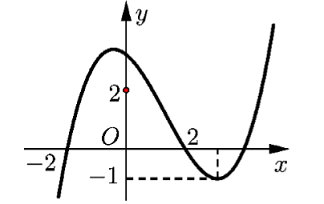
Số nghiệm của phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) với \(x \in \left( {0;\dfrac{{5\pi }}{2}} \right)\) là
- A \(4.\)
- B \(3.\)
- C \(5.\)
- D \(2.\)
Phương pháp giải:
Đặt \(2{\rm{cos}}\,x = t\), đánh giá nghiệm phương trình với ẩn t.
Lời giải chi tiết:
Đặt \(2{\rm{cos}}\,x = t\left( {t \in \left[ { - 2;2} \right]} \right)\). Phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) (1) trở thành \(f\left( {\left| t \right|} \right) = 1\) (2)
Dựng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) ta thấy, với \( - 2 \le x \le 2\) thì đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 1\) tại 2 điểm \({x_0}\,,\,\, - {x_0}\,\,\left( {0 < {x_0} < 2} \right)\)
Cho \(2{\rm{cos}}\,x = {x_0} \Rightarrow {\rm{cos}}\,x = \dfrac{{{x_0}}}{2} \in \left( {0;1} \right)\)
\( \Rightarrow \) Phương trình có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\,\,\) \(\left( {0 < {x_1} < \dfrac{\pi }{2},\,\,\dfrac{{3\pi }}{2} < {x_2} < 2\pi < {x_3} < \dfrac{{5\pi }}{2}} \right)\)
Cho \(2{\rm{cos}}\,x = - {x_0} \Rightarrow {\rm{cos}}\,x = - \dfrac{{{x_0}}}{2} \in \left( { - 1;0} \right)\)
\( \Rightarrow \) Phương trình có 2 nghiệm phân biệt \({x_4},{x_5}\,\,\left( {\dfrac{\pi }{2} < {x_4} < \pi < {x_5} < \dfrac{{3\pi }}{2}} \right)\)
Vậy số nghiệm của phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) với \(x \in \left( {0;\dfrac{{5\pi }}{2}} \right)\) là : \(5\).
Chọn C.







