Lời giải chi tiết:

ĐKXĐ: \(\left\{ \begin{array}{l} - {x^2} + 4x - 6m \ge 0\\ - {x^2} - 2x + m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le \dfrac{{ - {x^2} + 4x}}{6}\\m \ge {x^2} + 2x\end{array} \right.\)

Ta dựng 2 parabol như hình vẽ : \(y = \dfrac{{ - {x^2} + 4x}}{6}\left( {{P_1}} \right)\) (màu đỏ), \(y = {x^2} + 2x\,\left( {{P_2}} \right)\) (màu xanh)

Các đỉnh của parabol : \(A\left( {2;\dfrac{2}{3}} \right),\,B\left( { - 1; - 1} \right)\)

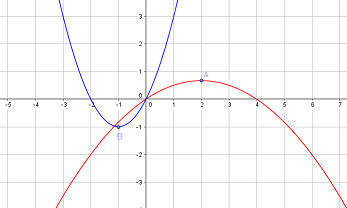
Để hàm số \(y = \sqrt { - {x^2} + 4x - 6m}  + \sqrt { - {x^2} - 2x + m} \) xác định tại đúng một điểm thì \(m = \dfrac{2}{3}\) hoặc \(m =  - 1\)

Chọn B.