 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
Cho hàm số \(y = f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau
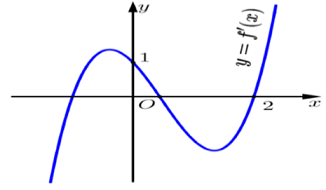
Bất phương trình \(f\left( x \right) < x + m\) có nghiệm với mọi \(x \in \left( {0;2} \right]\) khi và chỉ khi
- A \(m \ge f\left( 2 \right) - 2\).
- B \(m \le f\left( 0 \right)\).
- C \(m > f\left( 2 \right) - 2\).
- D \(m < f\left( 0 \right)\).
Phương pháp giải:
- Cô lập \(m\).
- Bất phương trình dạng \(g\left( x \right) < m\) có nghiệm với mọi \(x \in \left( {0;2} \right]\)khi và chỉ khi \(m > \mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right)\).
- Lập BBT hoặc sử dụng phương pháp hàm số xác định \(\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right)\).
Lời giải chi tiết:
Ta có : \(f\left( x \right) < x + m \Leftrightarrow f\left( x \right) - x < m\)
Xét hàm số \(g\left( x \right) = f\left( x \right) - x\)với \(x \in \left( {0;2} \right]\)ta có: \(g'\left( x \right) = f'\left( x \right) - 1 < 0\,\,\forall x \in \left( {0;2} \right].\)
\( \Rightarrow \) Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( {0;2} \right]\)\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = g\left( 2 \right) = f\left( 2 \right) - 2\)
Để bất phương trình \(f\left( x \right) < x + m\) có nghiệm với mọi \(x \in \left( {0;2} \right]\) thì \(m > f\left( 2 \right) - 2.\)
Chọn C.






