Phương pháp giải:

- Khối hộp chữ nhật có 3 độ dài là a, b, c có độ dài đường chéo là: \(\sqrt {{a^2} + {b^2} + {c^2}} \) và thể tích \(V = abc\).

- Biến đổi, rút tích \(ab\) theo \(c\).

- Chặn giá trị của \(c\).

- Sử dụng phương pháp hàm số để tìm GTLN.

Lời giải chi tiết:

Không mất tính tổng quát, giả sử khối hộp chữ nhật đó có 3 độ dài là a, b, c , trong đó: \(a \ge b \ge c\)

Theo đề bài, ta có: \(\left\{ \begin{array}{l}\left( {a + b + c} \right).4 = 40\\\sqrt {{a^2} + {b^2} + {c^2}}  = 5\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b + c = 10\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{a^2} + {b^2} + {c^2} = 50\,\,\left( 2 \right)\end{array} \right.\)

\(\begin{array}{l}\left( 2 \right) \Leftrightarrow {\left( {a + b} \right)^2} - 2ab + {c^2} = 50\\\,\,\,\,\,\, \Leftrightarrow {\left( {10 - c} \right)^2} - 2ab + {c^2} = 50\,\\\,\,\,\,\,\, \Leftrightarrow 2ab = {\left( {10 - c} \right)^2} + {c^2} - 50\\\,\,\,\,\,\, \Leftrightarrow ab = \dfrac{1}{2}\left[ {{{\left( {10 - c} \right)}^2} + {c^2} - 50} \right]\\ \Rightarrow {V_{hh}} = abc = \dfrac{1}{2}\left[ {{{\left( {10 - c} \right)}^2} + {c^2} - 50} \right]c\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {c^3} - 10{c^2} + 25c\end{array}\)

Do \(a + b + c = 10,\) mà \(a + b + c \ge 3c \Leftrightarrow c \le \dfrac{{10}}{3}.\)

Xét hàm số \(f\left( c \right) = {c^3} - 10{c^2} + 25c\)với \(c \in \left( {0;\dfrac{{10}}{3}} \right)\)ta có:

 \(f'\left( c \right) = 3{c^2} - 20c + 25,\,\,f'\left( c \right) = 0 \Leftrightarrow \left[ \begin{array}{l}c = 5\,\,\,\,\left( {ktm} \right)\\c = \dfrac{5}{3}\,\,\,\,\left( {tm} \right)\end{array} \right.\)

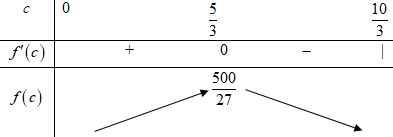
\( \Rightarrow \mathop {\max }\limits_{\left( {0;\dfrac{{10}}{3}} \right)} f\left( c \right) = f\left( {\dfrac{5}{3}} \right) = \dfrac{{500}}{{27}}\)

Với \(c = \dfrac{5}{3} \Rightarrow \)\(\left\{ \begin{array}{l}a + b = \dfrac{{25}}{3}\\{a^2} + {b^2} = \dfrac{{425}}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{25}}{3} - a\\{a^2} + {\left( {\dfrac{{25}}{3} - a} \right)^2} = \dfrac{{425}}{9}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{25}}{3} - a\\9{a^2} - 75a + 100 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{25}}{3} - a\\\left[ \begin{array}{l}b = \dfrac{5}{6}\\b = \dfrac{{20}}{3}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \dfrac{{20}}{3}\\b = \dfrac{5}{3}\end{array} \right.\,\,\,\left( {tm} \right)\\\left\{ \begin{array}{l}a = \dfrac{5}{3}\\b = \dfrac{{20}}{3}\end{array} \right.\,\,\,\,\left( {ktm} \right)\end{array} \right.\)

Vậy, thể tích của khối hộp chữ nhật lớn nhất là \({V_{{\rm{max}}}} = \dfrac{{500}}{{27}}\), khi hình hộp chữ nhật có 3 độ dài là \(\dfrac{5}{3};\dfrac{5}{3};\dfrac{{20}}{3}\).

Chọn A.