Phương pháp giải:

Sử dụng bảng biến thiên

Lời giải chi tiết:

ĐKXĐ: \( - 2 \le x \le 2\).

Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = x + \sqrt {4 - {x^2}} \) và đường thẳng \(y = m\).

Xét hàm số \(y = x + \sqrt {4 - {x^2}} \) ta có:

\(\begin{array}{l}y' = 1 - \dfrac{x}{{\sqrt {4 - {x^2}} }} = \dfrac{{\sqrt {4 - {x^2}}  - x}}{{\sqrt {4 - {x^2}} }}\\y' = 0 \Leftrightarrow \sqrt {4 - {x^2}}  - x \Leftrightarrow \sqrt {4 - {x^2}}  = x\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\4 - {x^2} = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 2\end{array} \right. \Leftrightarrow x = \sqrt 2 \end{array}\)

Bảng biến thiên:

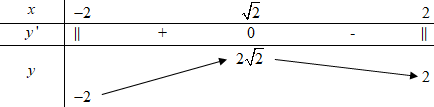
Vậy phương trình \(x + \sqrt {4 - {x^2}}  = m\) có nghiệm khi và chỉ khi \( - 2 \le m \le 2\sqrt 2 .\)

Chọn D.