Phương pháp giải:

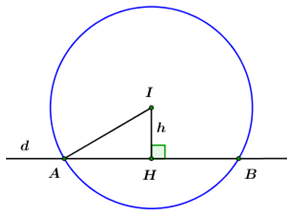
+) \(d\) cắt đường tròn \(\left( C \right)\) theo dây cung có độ dài \(l\) nên khoảng cách từ tâm đường tròn đến \(d\) là\(h = \sqrt {{R^2} - {{\left( {\frac{l}{2}} \right)}^2}} .\)

Lời giải chi tiết:

Giả sử phương trình đường thẳng \(d\) cần tìm và đi qua điểm \(\left( {1;2} \right)\) là \(d:a\left( {x - 1} \right) + b\left( {y - 2} \right) = 0\)\( \Leftrightarrow ax + by - a - 2b = 0\,\,\,\,\left( {{a^2} + {b^2} > 0} \right)\)

Vì \(d\) cắt \(\left( C \right)\) theo dây cung có độ dài  \(l = 8\) nên khoảng cách từ tâm \(I\left( {2; - 1} \right)\) của \(\left( C \right)\) đến \(d\) là:

\(IH = \sqrt {{R^2} - {{\left( {\frac{l}{2}} \right)}^2}}  = \sqrt {25 - {4^2}}  = 3.\)

\( \Rightarrow d\left( {I,d} \right) = \left| {\frac{{2a - b - a - 2b}}{{\sqrt {{a^2} + {b^2}} }}} \right| = 3\)\( \Leftrightarrow \left| {a - 3b} \right| = 3\sqrt {{a^2} + {b^2}} \)

\( \Leftrightarrow 8{a^2} + 6ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a =  - \frac{3}{4}b\end{array} \right.\)

+) \(a = 0\); chọn \(b = 1\) suy ra \(d:y - 2 = 0\)

+) \(a = 3;\,\,\,b =  - 4\)\( \Rightarrow d:3x - 4y + 5 = 0\)

Chọn  C.