Câu hỏi
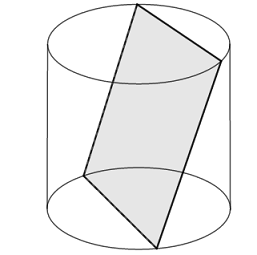
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng \(10cm\). Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
- A \(250c{m^2}\)
- B \(200c{m^2}\)
- C \(150c{m^2}\)
- D \(300c{m^2}\)
Phương pháp giải:
Khi bỏ miếng bìa hình vuông vào chiếc hộp như giả thiết ta thấy đoạn thẳng nối tâm 2 đáy của chiếc hộp cắt miếng bìa tại trung điểm của nó và là tâm của miếng bìa.
Tính độ dài cạnh của miếng bìa.
Lời giải chi tiết:
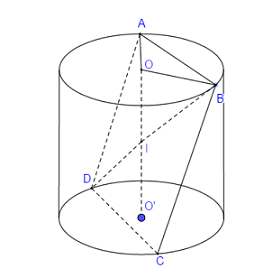
Gọi tâm 2 đáy của chiếc hộp hình trụ là \(O\) và \(O'\), miếng bìa hình vuông là \(ABCD\) với \(AB\) là dây cung của đường tròn tâm \(O\) còn \(CD\) là dây cung của đường tròn tâm \(O'\) như trong hình vẽ
Do đặt miếng bìa không song song với trục của hộp nên gọi \(I\)là giao điểm của \(OO'\) và miếng bìa \(ABCD\).
Ta thấy \(I\) chính là trung điểm của \(OO'\) và là tâm của miếng bìa \(ABCD\)
Do đó \(IO = \dfrac{1}{2}OO' = 5\left( {cm} \right);OB = OA = R = 10\left( {cm} \right)\)
\(OO'\) vuông góc với 2 đáy hay \(IO \bot OB\)
Tam giác \(IOB\) vuông tại \(O\) nên \(IB = \sqrt {I{O^2} + O{B^2}} = \sqrt {{5^2} + {{10}^2}} = 5\sqrt 5 \left( {cm} \right)\)
Suy ra \(BD = 2IB = 10\sqrt 5 \left( {cm} \right)\)
Ta có: \(A{D^2} + A{B^2} = B{D^2} \Rightarrow AD = \dfrac{{BD}}{{\sqrt 2 }} = 5\sqrt {10} \left( {cm} \right)\)
Diện tích của miếng bìa hình vuông là \(S = A{D^2} = 250\left( {c{m^2}} \right)\)
Chọn A.







