Phương pháp giải:

Khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\) là khoảng cách từ một điểm nằm trên \(a\) đến mặt phẳng \(\left( \alpha  \right)\) chứa đường thẳng \(b\) và song song với đường thẳng \(a\)

Tìm góc tạo bởi \(AB\) và mặt phẳng chứa đường tròn đáy.

Tìm đường cao của hình trụ qua khoảng cách giữa \(AB\) và \(OO'\)

Thể tích của khối trụ có bán kính đáy bằng \(a\) và chiều cao bằng \(h\) là  \(V = \pi {r^2}h\)

Lời giải chi tiết:

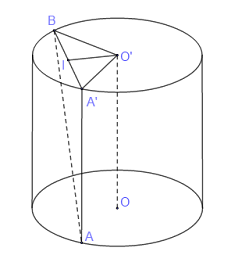
Giả sử \(A\) nằm trên đường tròn tâm \(O,\)\(B\) nằm trên đường tròn tâm \(O'\)

Qua \(A\) kẻ đường thẳng \(AA'//OO'\) (\(A'\) nằm trên đường tròn tâm \(O'\)). Gọi \(I\) là trung điểm của \(A'B\)

\(AA'//OO' \Rightarrow AA' \bot \left( {O'A'B} \right) \Rightarrow AA' \bot O'I\)

Tam giác \(O'A'B\) có \(O'A' = O'B = r\) nên tam giác \(O'A'B\) cân tại \(O'\) hay \(O'I \bot A'B\)

Suy ra \(O'I \bot \left( {A'AB} \right)\)

Do \(AA'//OO'\) nên khoảng cách giữa hai đường thẳng \(AB\) và \(OO'\) là khoảng cách từ \(O'\) đến mặt phẳng \(\left( {AB'A'} \right)\). Hay \(O'I = \dfrac{{a\sqrt 2 }}{2}\)

Ta có: \(IA' = \sqrt {O'A{'^2} - O'{I^2}}  = \sqrt {{a^2} - {{\left( {\dfrac{{\sqrt 2 a}}{2}} \right)}^2}}  = \dfrac{{\sqrt 2 a}}{2}\)

Góc tạo bởi \(AB\) và mặt phẳng chứa đường tròn đáy là góc giữa \(AB\) và \(A'B\)(do \(AA'\) vuông góc với 2 đáy).

Do đó \(\widehat {ABA'} = 45^\circ  \Rightarrow AA' = A'B = 2IA' = \sqrt 2 a\)

Vậy thể tích của hình trụ đã cho bằng \(V = \pi .O{A^2}.AA{'^2} = \pi .{a^2}.\sqrt 2 a = \sqrt 2 \pi {a^3}\)

Chọn B.