Câu hỏi
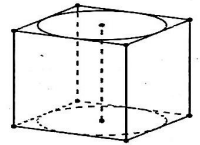
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương (tham khảo hình vẽ bên). Gọi \({S_1};{S_2}\) lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính \(S = {S_1} + {S_2}\left( {c{m^2}} \right)\).
- A \(S = 4\left( {2400 + 3\pi } \right)\)
- B \(S = 2400\left( {4 + 3\pi } \right)\).
- C \(S = 4\left( {2400 + \pi } \right)\)
- D \(S = 2400\left( {4 + \pi } \right)\)
Phương pháp giải:
Áp dụng công thức tính diện tích toàn phần của hình lập phương và hình trụ rồi suy ra tổng.
Lời giải chi tiết:
Hình lập phương có cạnh bằng 40cm do đó diện tích toàn phần là \({S_1} = {6.40^2} = 9600\,\,\left( {c{m^2}} \right).\)
Hình trụ có đáy là hình tròn nội tiếp hình vuông cạnh 40cm nên \(r = 20cm\);\(h = 40cm\).
\( \Rightarrow {S_2} = 2\pi {r^2} + 2\pi rh = 2\pi {.20^2} + 2\pi .20.40 = 2400\pi \,\,\left( {c{m^2}} \right).\)
\( \Rightarrow {S_1} + {S_2} = 9600 + 2400\pi = 2400\left( {4 + \pi } \right).\)
Chọn D.







