Phương pháp giải:

Từ giả thiết ta lập luận để có \(a > 0.\)

Từ đó tìm được các điểm cực trị của hàm số và suy ra được GTNN thông qua BBT.

Lời giải chi tiết:

Ta có: \(y' = 4a{x^3} + 2bx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\4a{x^2} + 2b = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} =  - \dfrac{b}{{2a}}\end{array} \right.\)

Tù giả thiết suy ra \(a > 0\).

TH1: Nếu \(b \ge 0\) thì hàm số có 1 cực trị \(x = 0.\) Suy ra hàm số đơn điệu trên \(\left( { - \infty ;0} \right)\) điều này mâu thuẫn với giả thiết \(\mathop {\min }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = f\left( { - 1} \right)\) nên ta loại TH này.

TH2: \(b < 0\) hàm số có ba cực trị \({x_1} = 0,{x_2} =  - \sqrt {\dfrac{{ - b}}{{2a}}} ,{x_3} = \sqrt {\dfrac{{ - b}}{{2a}}} \)

Vì \(\mathop {\min }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = f\left( { - 1} \right)\) nên hàm số đạt cực tiểu tại \(x =  - 1 \Rightarrow {x_2} =  - 1;{x_3} = 1\), khi đó \(a > 0.\)

Ta có BBT:

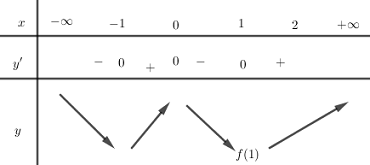
Từ BBT suy ra GTNN của hàm số trên \(\left[ {0;2} \right]\) là \(f\left( 1 \right) = a + b + c\)

Lại có \(x = 1\) là cực trị của hàm số nên \( - \dfrac{b}{{2a}} = 1 \Rightarrow b =  - 2a\)

Suy ra \(f\left( 1 \right) = a + \left( { - 2a} \right) + c = c - a\)

Vậy GTNN cần tìm là \(c - a.\)

Chọn B.