Câu hỏi
Cho mặt cầu \(S(I;R)\) và mặt phẳng \((P)\) cách \(I\) một khoảng bằng \(\dfrac{R}{2}\). Khi đó thiết diện của \((P)\) và \(\left( S \right)\) là một đường tròn có bán kính bằng:
- A \(R\).
- B \(\dfrac{{R\sqrt 3 }}{2}\).
- C \(R\sqrt 3 \)
- D \(\dfrac{R}{2}\)
Phương pháp giải:
Gọi \(R\) là bán kính mặt cầu\(\left( S \right),\)\(d = d\left( {I;\,\,\left( P \right)} \right)\) là khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\) và \(r\) là bán kính đường tròn giao tuyến mà \(\left( P \right)\) cắt \(\left( S \right).\) Khi đó ta có: \(r = \sqrt {{R^2} - {d^2}} .\)
Lời giải chi tiết:
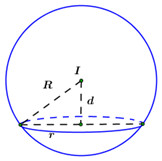
Áp dụng công thức: \(r = \sqrt {{R^2} - {d^2}} \) ta có:
\(r = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}} = \sqrt {\dfrac{{3{R^2}}}{4}} = \dfrac{{R\sqrt 3 }}{2}.\)
Chọn B.
Câu hỏi trước
