Phương pháp giải:

Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(IA = IB = IC = IM = IN\).

Lời giải chi tiết:

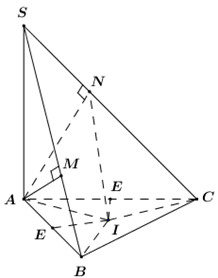
Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC \Rightarrow IA = IB = IC\,\,\left( 1 \right)\).

Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,AC\) ta có:

\(\left\{ \begin{array}{l}IE \bot AC\\IE \bot SA\end{array} \right. \Rightarrow IE \bot \left( {SAC} \right) \Rightarrow IE \bot \left( {ANC} \right)\).

Lại có \(E\) là tâm đường tròn ngoại tiếp tam giác \(ANC\) (do tam giác \(ANC\) vuông tại \(N\))

Do đó \(IE\) là trục của \(\Delta ANC \Rightarrow IA = IC = IN\,\,\left( 2 \right)\).

Chứng minh tương tự ta có \(IE\) là trục của tam giác \(AMB\)

\( \Rightarrow IA = IB = IM\,\,\left( 3 \right)\).

Từ (1), (2) và (3) \( \Rightarrow IA = IB = IC = IM = IN \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(ABCMN\), bán kính mặt cầu ngoại tiếp này là \(R = IA\), chính là bán kính mặt cầu ngoại tiếp tam giác \(ABC\).

Ta có \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC = \dfrac{1}{2}.3.2.\sin {60^0} = \dfrac{{3\sqrt 3 }}{2}\).

Áp dụng định lí Cô-sin trong tam giác \(ABC\) ta có

\(BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos \angle BAC}  = \sqrt {{3^2} + {2^2} - 2.3.2.\cos {{60}^0}}  = \sqrt 7 \).

 Vậy \(R = \dfrac{{AB.BC.CA}}{{4{S_{\Delta ABC}}}} = \dfrac{{3.\sqrt 7 .2}}{{4.\dfrac{{3\sqrt 3 }}{2}}} = \dfrac{{\sqrt {21} }}{3}\).

Chọn B.