Lời giải chi tiết:

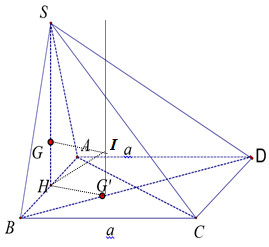
\( + )\)Xét \(\Delta SAB\)đều: Gọi \(H\) là trung điểm \(AB \Rightarrow SH \bot \left( {ABCD} \right)\) và \(SH = \dfrac{{a\sqrt 3 }}{2}\).

Gọi \(G\) là trọng tâm \(\Delta SAB\) ta có:

\(\dfrac{{SG}}{{SH}} = \dfrac{2}{3} \Rightarrow SG = \dfrac{2}{3}SH = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2}a = \dfrac{{\sqrt 3 }}{3}a = GA = GB\)

\( + )\)Xét \(\Delta ABC\)có:\(\left\{ \begin{array}{l}BA = BC\\\widehat {ABC} = {60^0}\end{array} \right. \Rightarrow \Delta ABC\)đều.

Gọi \(O = AC \cap BD \Rightarrow BO = \dfrac{{a\sqrt 3 }}{2}\).

Gọi \(G'\) là trọng tâm \(\Delta ABC\), kẻ đường thẳng \(d \bot \left( {ABC} \right)\) tại \(G'\).

Trong \(\left( {SH;d} \right)\) kẻ \(GI\parallel HG'\,\,\left( {I \in d} \right)\).

\( \Rightarrow GI \bot \left( {SAB} \right)\).

\( \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).

Ta có: Tam giác \(ABC\) đều cạnh \(a \Rightarrow HG' = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\).

\(\Delta SAB\) đều cạnh \(a \Rightarrow GH = \dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6} = G'I\).

\( \Rightarrow \Delta HIG'\) vuông cân tại \(G' \Rightarrow HI = HG'\sqrt 2  = \dfrac{{a\sqrt 3 }}{6}.\sqrt 2  = \dfrac{{a\sqrt 6 }}{6}\).

Ta có: \(\left\{ \begin{array}{l}AB \bot GH\\AB \bot HG'\end{array} \right. \Rightarrow AB \bot \left( {SH;d} \right) \Rightarrow AB \bot HI\).

Xét tam giác vuông \(AHI\) có: \(IA = \sqrt {I{H^2} + A{H^2}}  = \sqrt {\dfrac{{{a^2}}}{6} + \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt {15} }}{6}\).

\( \Rightarrow S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{\sqrt {15} }}{6}a} \right)^2} = \dfrac{5}{3}{a^2}\pi .\)

Chọn B.