Câu hỏi
Cho hình trụ có bán kính \(R\). Gọi \(AB,\,\,CD\) lần lượt là hai dây cung song song với nhau và nằm trên hai đường tròn đáy có cùng độ dài là \(R\sqrt 2 \). Mặt phẳng \(\left( {ABCD} \right)\) không song song và cũng không chứa trục của hình trụ. Góc giữa \(\left( {ABCD} \right)\) và đáy bằng \({30^0}\). Tính \(V\) của hình trụ?
- A \(\dfrac{{\pi {R^3}\sqrt 6 }}{3}\)
- B \(\dfrac{{\pi {R^3}\sqrt 6 }}{2}\)
- C \(\dfrac{{\pi {R^3}\sqrt 6 }}{6}\)
- D \(\dfrac{{\pi {R^3}\sqrt 2 }}{3}\)
Lời giải chi tiết:
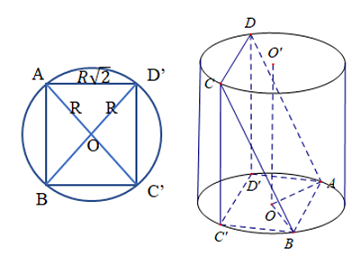
\( + \)Kẻ \(CC'\) vuông đáy tại \(C'\).
\(DD'\) vuông đáy tại \(D'\).
\( \Rightarrow ABC'D'\) là hình bình hành (Do \(CD\parallel C'D'\parallel AB\))
\( + \)\(\Delta OAB\)có: \(O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2}\) . Mà\(A{B^2} = 2{R^2}\)
\( \Rightarrow \Delta OAB\)vuông tại \(O\) (Định lí Pytago đảo) \( \Rightarrow AC' \bot BD'\)
\( + \)Ta thấy \(AC' = BD' = 2R\) (Vì tứ giác \(ABC'D'\) nội tiếp đường tròn)
\( \Rightarrow ABC'D'\)là hình vuông \( \Rightarrow AB = AD' = BC' = C'D' = R\sqrt 2 \).
\( + \)Góc \(\left( {ABCD} \right)\) và (đáy) bằng \({30^0} \Rightarrow \widehat {\left( {\left( {ABCD} \right);\left( {day} \right)} \right)} = \widehat {D'AD} = {30^0}\)
\( + \)Xét \({\Delta _v}DAD'\) có: \(\tan {30^0} = \dfrac{{DD'}}{{D'A}} \Rightarrow DD' = R\sqrt 2 .\dfrac{{\sqrt 3 }}{3} = R\dfrac{{\sqrt 6 }}{3}\).
\( \Rightarrow \)Vtrụ \( = \pi {R^2}.\dfrac{{R\sqrt 6 }}{3} = \dfrac{{\pi {R^3}\sqrt 6 }}{3}\).
Chọn A







