Lời giải chi tiết:

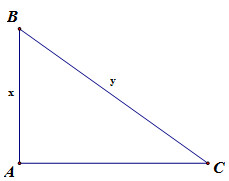
Giả sử \(\Delta ABC\)có \(\widehat A = {90^0};\,\,AB = x;\,\,BC = y\)

Có: \(x + y = a \Leftrightarrow y = a - x\)

Xét \(\Delta ABC\,\,\,\,\left( {\widehat A = {{90}^0}} \right)\) có:

\(\eqalign{
& A{B^2} + A{C^2} = B{C^2}\,\left( {Pytago} \right) \cr
& \Leftrightarrow {x^2} + A{C^2} = {\left( {a - x} \right)^2} \cr
& \Leftrightarrow A{C^2} = {\left( {a - x} \right)^2} - {x^2} \cr
& \Leftrightarrow AC = \sqrt {{{\left( {a - x} \right)}^2} - {x^2}} \cr
& {S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.x.\sqrt {{{\left( {a - x} \right)}^2} - {x^2}} \cr}\)

\(a = 1 \Rightarrow y = \dfrac{1}{2}.x.\sqrt {1 - 2x} \)

Xét \(y = \dfrac{1}{2}.x.\sqrt {{{\left( {a - x} \right)}^2} - {x^2}} \)

Giả sử coi hằng số

TXĐ: \(D = \left( {0;\dfrac{1}{2}} \right]\)

Dùng máy tính cầm tay: ấn tổ hợp phím MODE + 7

Nhập \(\left\{ \begin{array}{l}f\left( x \right) = \dfrac{1}{2}.x.\sqrt {1 - 2x} \\Start:0\\End:\dfrac{1}{2}\\Step:\dfrac{{End - Start}}{{19}} = \dfrac{1}{2}:19\end{array} \right.\)

Nhìn vào cột \(f\left( x \right)\)thấy \(max\,f\left( x \right) = 0,0961 \approx \dfrac{1}{{6\sqrt 3 }}\)

Chọn C.