Môn Toán - Lớp 12
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
Cho một tấm nhôm hình vuông cạnh \(2016\left( {cm} \right)\). Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\left( {cm} \right)\), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm \(x\) để hộp nhận được có thể tích lớn nhất.
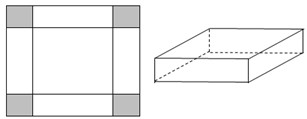
- A \(x = 336\).
- B \(x = 504\).
- C \(x = 672\).
- D \(x = 1008\).
Lời giải chi tiết:
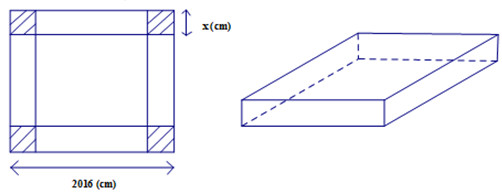
\(V = x\left( {2016 - 2x} \right)\left( {2016 - 2x} \right)\)
ĐKXĐ: \(\left\{ \begin{array}{l}x > 0\\2016 - 2x > 0\end{array} \right. \Leftrightarrow 0 < x < 1008\)
Xét \(y = x\left( {2016 - 2x} \right)\left( {2016 - 2x} \right) = x{\left( {2016 - 2x} \right)^2}\)
\(\,\,\,\,\,\,\,\,\,\,\,\,\, = x\left[ {{{\left( {2016} \right)}^2} - 8064 + 4{x^2}} \right] = 4{x^3} - 8064{x^2} + {\left( {2016} \right)^2}x\)
\(y' = 12{x^2} - 16128x + {\left( {2016} \right)^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1008\,\,\,\,\left( L \right)\\x = 336\,\,\,\,\left( {TM} \right)\end{array} \right.\)
BBT:
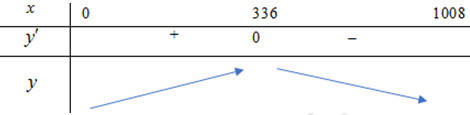
\(\Rightarrow \) Để thể tích hộp lớn nhất thì \(x=336\).
Chọn A.
Câu hỏi trước
