Môn Toán - Lớp 12
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
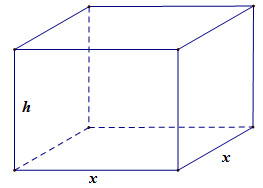
Một hộp không nắp được làm từ một mảnh các tông theo hình mẫu. Hộp có đáy là một hình vuông cạnh \(x\left( {cm} \right)\), chiều cao \(h\left( {cm} \right)\) và có thể tích là \(500\left( {c{m^3}} \right)\). Hãy tìm độ dài cạnh của hình vuông sao cho chiếc hộp được làm ra tốn ít nhiên liệu nhất.
- A \(5\,\,cm\)
- B \(10\,\,cm\)
- C \(2\,\,cm\)
- D \(3\,\,cm\)
Lời giải chi tiết:
\(V = h.{x^2} = 500 \Leftrightarrow h = \dfrac{{500}}{{{x^2}}}\)
\({S_{tp}} = 4xh + {x^2} = 4x\dfrac{{500}}{{{x^2}}} + {x^2} = \dfrac{{2000}}{x} + {x^2}\)
Để chiếc hộp làm ra tốn ít nguyên liệu nhất
\( \Rightarrow \)Tìm\(\min y = \dfrac{{2000}}{x} + {x^2}\)
TXĐ: \(D = \left( {0; + \infty } \right)\)
Dung máy tính cầm tay: ấn tổ hợp phím mode +7
Nhập: \(\left\{ \begin{array}{l}f\left( x \right) = \dfrac{{2000}}{x} + {x^2}\\start:0\\end:10\\step = \dfrac{{end - start}}{{19}} = \dfrac{{10}}{{19}}\end{array} \right.\)
Nhìn vào cột \(F\left( x \right)\)thấy \(\min \,f\left( x \right) = 300\)tại \(x = 10\)
Chọn B.
Câu hỏi trước
