Lời giải chi tiết:

Xét \(y = {x^2} - 2x + m \Rightarrow y' = 2x - 2 = 0 \Rightarrow x = 1\) (thỏa mãn)

Thay \(x =  - 1 \Rightarrow \) \(y\left( { - 1} \right) = \left| {m + 3} \right|\)

Thay \(x = 1 \Rightarrow \)\(y\left( 1 \right) = \left| {m - 1} \right|\,\)

Thay \(x = 2 \Rightarrow \)\(y\left( 2 \right) = \left| m \right|\)

BBT:

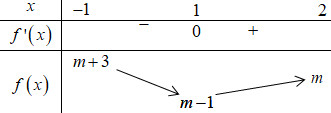
+ Đến đây ta không thể biết được giá trị nào max trong 3 giá trị trên \( \Rightarrow \) chia 3 TH của m

TH1: \(m - 1 \ge 0\) \( \Rightarrow \max \left| {f\left( x \right)} \right| = f\left( { - 1} \right) = m + 3\).

\( \Rightarrow m + 3 = 5 \Leftrightarrow m = 2\,\,\,\left( {tm} \right)\).

TH2: \(m - 1 < 0 \le m \Leftrightarrow 0 \le m < 1\).

\( \Rightarrow \max \left| {f\left( x \right)} \right| = \max \left\{ {m + 3;1 - m} \right\}\).

Do \(0 \le m < 1 \Rightarrow \left\{ \begin{array}{l}3 \le m + 3 < 4\\0 < 1 - m \le 1\end{array} \right. \Rightarrow m + 3 > 1 - m\,\,\forall m \in \left[ {0;1} \right)\).

\( \Rightarrow \max \left| {f\left( x \right)} \right| = m + 3 = 5 \Leftrightarrow m = 2\,\,\left( {ktm} \right)\).

TH3: \(m \le 0 \le m + 3 \Leftrightarrow  - 3 < m \le 0\).

\( \Rightarrow \max \left| {f\left( x \right)} \right| = \max \left\{ {m + 3;1 - m} \right\}\).

+ Nếu \(m + 3 \ge 1 - m \Leftrightarrow m \ge  - 1\), kết hợp điều kiện \( \Rightarrow  - 1 \le m \le 0\).

Khi đó \(\max \left| {f\left( x \right)} \right| = m + 3 = 5 \Leftrightarrow m = 2\,\,\left( {ktm} \right)\).

+ Nếu \(m + 3 < 1 - m \Leftrightarrow m <  - 1\), kết hợp điều kiện \( \Rightarrow  - 3 < m <  - 1\).

\( \Rightarrow \max \left| {f\left( x \right)} \right| = 1 - m = 5 \Leftrightarrow m =  - 4\,\,\left( {ktm} \right)\).

TH4: \(m + 3 \le 0 \Rightarrow m \le  - 3\).

Khi đó \(\max \left| {f\left( x \right)} \right| = 1 - m = 5 \Leftrightarrow m =  - 4\,\,\,\left( {tm} \right)\).

Vậy có 2 giá trị là \(m = 2,\,\,\,m =  - 4.\)

Chọn C.