Câu hỏi
Một vật trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng dài 10m nghiêng 300 so với phương ngang. Hệ số ma sát trượt giữa vật và mặt phẳng nghiêng là 0,2. Cho g = 10m/s2
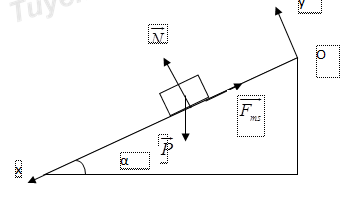
a) Vẽ các lực tác dụng lên vật khi trượt, tính gia tốc của vật?
b) Tìm vận tốc khi vật đến chân mặt phẳng nghiêng?
c) Tính thời gian vật đi hết quãng đường 2m cuối trước khi đến chân mặt phẳng nghiêng?
Phương pháp giải:
a) Các lực tác dụng lên vật: Trọng lực, phản lực, lực ma sát.
b) Áp dụng công thức độc lập với thời gian :
\({v^2}--{v_0}^2 = 2as\)
c) Áp dụng công thức tính quãng đường :
\(S = {v_0}.t + \frac{1}{2}a.{t^2}\)
Tìm thời gian đi hết 8m và đi hết 10m, sau đó lấy t10 – t8
Lời giải chi tiết:
Tóm tắt:
l = 10m ; α = 300; μ = 0,2 ; g = 10m/s2
a) Vẽ các lực tác dụng lên vật khi trượt, tính gia tốc của vật?
b) Tìm vận tốc khi vật đến chân mặt phẳng nghiêng?
c) Tính thời gian vật đi hết quãng đường 2m cuối trước khi đến chân mặt phẳng nghiêng?
Giải :
a) Chọn hệ trục tọa độ Oxy như hình vẽ.
- Áp dụng định luật 2 Niuton:
\(\overrightarrow N + \overrightarrow P + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \)
Chiếu lên hai trục Ox và Oy ta được:
\(\left\{ \begin{array}{l}
N = P.cos\alpha \\
P.\sin \alpha - {F_{ms}} = m.a
\end{array} \right.\)
Mà \({F_{ms}} = \mu .N \Rightarrow a = \frac{{g.m.\sin \alpha - \mu .m.g.cos\alpha }}{m} = g.(sin\alpha - \mu .cos\alpha )\)
Vậy:\(a = g.\left( {sin{{30}^0} - \mu .cos{{30}^0}} \right) = 3,27\left( {m/{s^2}} \right)\)
b) Khi tới chân mặt phẳng nghiêng vật đi được quãng đường S = 10m.
Áp dụng công thức:
\({v^2} - {0^2} = 2as\; \Rightarrow v = 8,09m/s\) (do v0 = 0)
c) Thời gian vật đi hết S1 = 8m đầu tiên trên mặt nghiêng là t1,
Ta có:
\({S_1} = \frac{1}{2}.a.t_1^2 \Rightarrow {t_1} = \sqrt {\frac{{2.{S_1}}}{a}} = \sqrt {\frac{{2.8}}{{3,27}}} = 2,21s\)
Thời gian vật đi hết S = 10m trên mặt nghiêng là t, tính được t:
Áp dụng công thức
\(S = \frac{1}{2}.a.{t^2} \Rightarrow t = \sqrt {\frac{{2.S}}{a}} = \sqrt {\frac{{2.10}}{{3,27}}} = 2,47s\)
Thời gian vật đi hết 2m cuối trên mặt nghiêng là:
\(\Delta t{\rm{ }} = t--{t_1} = 2,47 - 2,21 = 0,26\left( s \right)\)