Câu hỏi
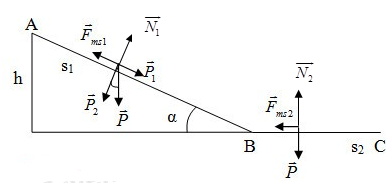
Một vật có m = 2kg trượt không vận tốc ban đầu trên mặt phẳng nghiêng nhẵn, dài 10m, chiều cao 5m. Lấy g = 10m/s2 ; hệ số ma sát trên mặt phẳng nghiêng là µ1 = 0,25.
a) Tính gia tốc của vật trên mặt phẳng nghiêng và vận tốc của vật tại chân mặt phẳng nghiêng.
b) Khi xuống hết mặt phẳng nghiêng, vật tiếp tục chuyển động trên mặt phẳng ngang, hệ số ma sát là µ2 = 0,5. Tính quãng đường từ lúc vật bắt đầu chuyển động trên mặt phẳng ngang cho đến khi dừng hẳn.
- A a) a1 = 2,835m/s2 ; vB = 7,53m/s – b) s2 = 5,67m
- B a) a1 = 2,835m/s2 ; vB = 7,53m/s – b) s2 = 9,94m
- C a) a1 = 5m/s2 ; vB = 10m/s – b) s2 = 5,67m
- D a) a1 = 5m/s2 ; vB = 10m/s – b) s2 = 9,94m
Phương pháp giải:
Phương pháp động lực học:
Bước 1: Chọn vật (hệ vật) khảo sát.
Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động)
Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ.
Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn.
\(\overrightarrow {{F_{hl}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = m.\overrightarrow a \) (*) (Tổng tất cả các lực tác dụng lên vật)
Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy:
Ox: F1x + F2x + … + Fnx = ma (1)
Oy: F1y + F2y + … + Fny = 0 (2)
Giải phương trình (1) và (2) ta thu được đại lượng cần tìm
Lời giải chi tiết:
m = 2kg ; v0 = 0 ; s1 = 10m ; h = 5m ; g = 10m/s2; µ1 = 0,25; µ2 = 0,5.
a) Ta có: \(\sin \alpha = \dfrac{h}{{{s_1}}} = \dfrac{5}{{10}} = \dfrac{1}{2} \Rightarrow \alpha = {30^0}\)
Các lực tác dụng vào vật khi vật chuyển động trên mặt phẳng nghiêng: \(\overrightarrow P ;\overrightarrow {{F_{ms1}}} ;\overrightarrow {{N_1}} \)
Áp dụng định luật II Niu tơn ta có: \(\overrightarrow P + \overrightarrow {{F_{ms1}}} + \overrightarrow {{N_1}} = m\overrightarrow {{a_1}} \,\,\,\,\,\left( 1 \right)\)
Chiếu (1) lên Ox và Oy ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}P.sin\alpha - {F_{ms1}} = m{a_1}\\ - {\rm{ }}Pcos\alpha + N = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}N = P.\cos \alpha \Rightarrow {F_{ms1}} = {\mu _1}P.\cos \alpha \\P.sin\alpha - {F_{ms1}} = m{a_1}\,\end{array} \right.\\ \Rightarrow mg.sin\alpha - {\mu _1}mg.\cos \alpha = m{a_1}\\ \Rightarrow {a_1} = g.\left( {sin\alpha - {\mu _1}\cos \alpha } \right) = 10.\left( {\sin 30 - 0,25.\cos 30} \right) \approx 2,835m/{s^2}\end{array}\)
Vận tốc của vật tại chân mặt phẳng nghiêng:
\(v_B^2 - v_A^2 = 2{a_1}{s_1} \Rightarrow {v_B} = \sqrt {2{a_1}.{s_1}} = \sqrt {2.2,835.10} = 7,53m/s\)
b)
Các lực tác dụng vào vật khi vật chuyển động trên mặt phẳng ngang: \(\overrightarrow P ;\overrightarrow {{F_{ms2}}} ;\overrightarrow {{N_2}} \)
Áp dụng định luật II Niu tơn ta có: \(\overrightarrow P + \overrightarrow {{F_{ms2}}} + \overrightarrow {{N_2}} = m\overrightarrow {{a_2}} \,\,\,\,\,\left( 2 \right)\)
Chiếu (2) lên trục Ox ta có:
\( - {F_{ms2}} = m{a_2} \Rightarrow - {\mu _2}mg = m{a_2} \Rightarrow {a_2} = - {\mu _2}g = - 0,5.10 = - 5m/{s^2}\)
Giả sử đến C vật dừng lại.
Ta có :
\(\begin{gathered}
v_C^2 - v_B^2 = 2{a_2}{s_2} \Leftrightarrow 0 - v_B^2 = 2{a_2}{s_2} \hfill \\
\Rightarrow {s_2} = - \frac{{v_B^2}}{{2{a_2}}} = - \frac{{{{7,53}^2}}}{{2.\left( { - 5} \right)}} = 5,67m \hfill \\
\end{gathered} \)
Chọn A.