Phương pháp giải:

Phương pháp động lực học:

Bước 1: Chọn vật (hệ vật) khảo sát.

Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động)

Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ.

Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn.

\(\overrightarrow{{{F}_{hl}}}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+...+\overrightarrow{{{F}_{n}}}=m.\overrightarrow{a}\) (*) (Tổng tất cả các lực tác dụng lên vật)

Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy:

 Ox: F_1x + F_2x + … + F_nx = ma    (1)

 Oy: F_1y + F_2y + … + F_ny = 0    (2)

Giải phương trình (1) và (2) ta thu được đại lượng cần tìm

Lời giải chi tiết:

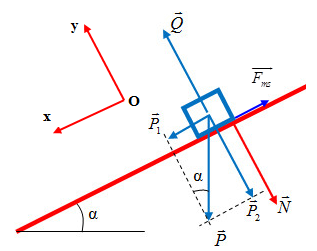
Vật chịu tác dụng của 3 lực trên mặt phẳng nghiêng:

+ Trọng lực \(\overrightarrow{P}\)

+ Phản lực \(\overrightarrow{Q}\)

 + Lực ma sát: \(\overrightarrow{{{F}_{ms}}}\)

Biểu diễn các lực tác dụng vào vật và chọn hệ trục toạ độ như hình vẽ:

Ta có: 

\(\left\{ \begin{array}{l}
\overrightarrow P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} \\
\left( {\overrightarrow {{P_2}} ;\overrightarrow P } \right) = \alpha
\end{array} \right.\)

Từ hình vẽ ta có: 

\(\left\{ \begin{array}{l}
\sin \alpha = \frac{{{P_1}}}{P} \Rightarrow {P_1} = P.\sin \alpha = mg.\sin \alpha \\
\cos \alpha = \frac{{{P_2}}}{P} \Rightarrow {P_2} = P.\cos \alpha = mg.\cos \alpha
\end{array} \right.\)

Áp dụng định luật II Niuton ta có :

\(\overrightarrow{{{F}_{ms}}}+\overrightarrow{Q}+\overrightarrow{{{P}_{1}}}+\overrightarrow{{{P}_{2}}}=m.\overrightarrow{a}\,\,\,\left( * \right)\)

Chiếu (*) lên Ox, Oy ta được :

\(\begin{array}{l}
\left\{ \begin{array}{l}
- {F_{ms}} + {P_1} = ma\\
Q - {P_2} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \frac{{{P_1} - {F_{ms}}}}{m}\\
Q = {P_2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \frac{{mg.\sin \alpha - \mu N}}{m}\\
N = Q = {P_2} = mg.\cos \alpha
\end{array} \right.\\
\Rightarrow a = \frac{{mg.\sin \alpha - \mu .mg.\cos \alpha }}{m} = g\left( {\sin \alpha - \mu .\cos \alpha } \right)
\end{array}\)

Thay số ta được : \(a=10.\left( \sin 30-0,2.\cos 30 \right)=3,27m/{{s}^{2}}\)

Ta có : \(v_{B}^{2}-v_{A}^{2}=2a.AB\Rightarrow {{v}_{B}}=\sqrt{v_{A}^{2}+2a.AB}=\sqrt{0+2.4,13.10}\approx 8,1m/s\)

Chọn B.