Phương pháp giải:

Qua M kẻ các đường thẳng song song với các cạnh D ABC. Sử dụng tính chất tam giác đều và quy tắc hình bình hành để biến đổi.

Lời giải chi tiết:

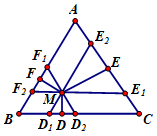
Qua \(M\) kẻ các đường thẳng song song với các cạnh của \(\Delta ABC:\) \({F_1},\,\,{F_2} \in AB;\,\,\,{E_1},\,\,{E_2} \in AC,\,\,\,{D_1},\,\,{D_2} \in BC\) sao cho \({F_1}{D_2}//DC,\,\,{D_1}{E_2}//AB,\,\,\,{F_2}{E_1}//BC.\)

Dễ thấy các tam giác đều \(M{D_1}{D_2},\,\,M{E_1}{E_2},\,\,M{F_1}{F_2}\) và các hình bình hành \(M{F_1}A{E_2},\,\,M{E_1}C{D_2},\,\,M{D_1}B{F_2}\).

Ta có: \(\overrightarrow {MD}  = \frac{1}{2}\left( {\overrightarrow {M{D_1}}  + {{\overrightarrow {MD} }_2}} \right),\,\,\overrightarrow {ME}  = \frac{1}{2}\left( {\overrightarrow {M{E_1}}  + \overrightarrow {M{E_2}} } \right),\,\,\overrightarrow {MF}  = \frac{1}{2}\left( {\overrightarrow {M{F_1}}  + \overrightarrow {M{F_2}} } \right)\)

Cộng từng vế 3 đẳng thức và nhóm  ta được:

\(\begin{array}{l}\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF}  = \frac{1}{2}\left( {\overrightarrow {M{D_1}}  + \overrightarrow {M{D_2}}  + \overrightarrow {M{E_1}}  + \overrightarrow {M{E_2}}  + \overrightarrow {M{F_1}}  + \overrightarrow {M{F_2}} } \right)\\ = \frac{1}{2}\left[ {\left( {\overrightarrow {M{D_1}}  + \overrightarrow {M{F_2}} } \right) + \left( {\overrightarrow {M{F_1}}  + \overrightarrow {M{E_2}} } \right) + \left( {\overrightarrow {M{E_1}}  + \overrightarrow {M{D_2}} } \right)} \right]\\ = \frac{1}{2}\left( {\overrightarrow {MB}  + \overrightarrow {MA}  + \overrightarrow {MC} } \right)\\ = \frac{1}{2}.3\overrightarrow {MO}  = \frac{3}{2}\overrightarrow {MO} .\end{array}\)         

Chọn  C.