Câu hỏi
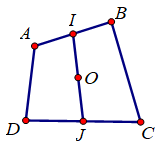
Cho tứ giác \(ABCD\), với M là điểm bất kì. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Khẳng định nào sau đây đúng?
- A \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MO} \)
- B \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MO} \)
- C \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MO} \)
- D \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
Phương pháp giải:
Áp dụng hệ thức trung điểm để chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \). Từ đó tách để suy ra đpcm.
Lời giải chi tiết:
Theo hệ thức trung điểm ta có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} ,\,\,\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {OJ} \)
Mặt khác \(O\) là trung điểm \(IJ \Rightarrow \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow 0 .\)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 2\left( {\overrightarrow {OI} + \overrightarrow {OJ} } \right) = \overrightarrow 0 .\)
Do đó với mọi điểm \(M\) thì:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MC} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MD} } \right) = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} .\end{array}\)
Chọn D.