Phương pháp giải:

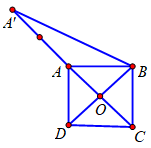
Gọi \(O\) là tâm hình vuông. Lấy điểm \(A'\) trên tia \(OA\)sao cho \(OA' = 3OA\). Áp dụng các quy tắc để biến đổi và tính \(\overrightarrow u \).

Lời giải chi tiết:

Gọi \(O\) là tâm hình vuông.

Theo quy tắc ba điểm ta có

\(\begin{array}{l}\overrightarrow u  = 4\overrightarrow {MA}  - 3\overrightarrow {MB}  + \overrightarrow {MC}  - 2\overrightarrow {MD} \\\,\,\,\,\, = 4\left( {\overrightarrow {MO}  + \overrightarrow {OA} } \right) - 3\left( {\overrightarrow {MO}  + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO}  + \overrightarrow {OC} } \right) - 2\left( {\overrightarrow {MO}  + \overrightarrow {OD} } \right)\\\,\,\,\,\, = 4\overrightarrow {OA}  - 3\overrightarrow {OB}  + \overrightarrow {OC}  - 2\overrightarrow {OD} \end{array}\)

Mà \(\overrightarrow {OD}  =  - \overrightarrow {OB} ,\,\,\overrightarrow {OC}  =  - \overrightarrow {OA} \)

\( \Rightarrow \overrightarrow u  = 4\overrightarrow {OA}  - 3\overrightarrow {OB}  + \overrightarrow {OC}  - 2\overrightarrow {OD}  = 4\overrightarrow {OA}  - 3\overrightarrow {OB}  - \overrightarrow {OA}  + 2\overrightarrow {OB}  = 3\overrightarrow {OA}  - \overrightarrow {OB} \)

Lấy điểm \(A'\) trên tia \(OA\)sao cho \(OA' = 3OA,\) khi đó: \(\overrightarrow {OA'}  = 3\overrightarrow {OA} \)

\( \Rightarrow \overrightarrow u  = \overrightarrow {OA'}  - \overrightarrow {OB}  = \overrightarrow {BA'} .\)

Mặt khác: \(BA' = \sqrt {O{B^2} + OA{'^2}}  = \sqrt {O{B^2} + 9O{A^2}}  = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + 9.{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = a\sqrt 5 \)

\( \Rightarrow \left| {\overrightarrow u } \right| = BA' = a\sqrt 5 .\)

 Chọn A.