Phương pháp giải:

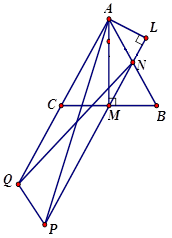
Gọi \(N\) là trung điểm \(AB\), \(Q\) là điểm đối xứng của \(A\) qua \(C\) và \(P\) là đỉnh của hình bình hành \(AQPN\)để áp dụng quy tắc hình bình hành. Gọi \(L\) là hình chiếu của \(A\) lên \(QN\) để tính.

Lời giải chi tiết:

Gọi \(N\) là trung điểm \(AB\), \(Q\) là điểm đối xứng của \(A\) qua \(C\) và \(P\) là đỉnh của hình bình hành \(AQPN\).

Khi đó ta có: \(\frac{1}{2}\overrightarrow {AB}  = \overrightarrow {AN} ,\,\,2\overrightarrow {AC}  = \overrightarrow {AQ} \)

Suy ra theo quy tắc hình bình hành ta có:  \(\frac{1}{2}\overrightarrow {AB}  + 2\overrightarrow {AC}  = \overrightarrow {AN}  + \overrightarrow {AQ}  = \overrightarrow {AP} \)

Gọi \(L\) là hình chiếu của \(A\) lên  \(PN.\)

Vì  \(MN//AC \Rightarrow \angle ANL = \angle MNB = \angle CAB = {60^0}\)

Xét tam giác vuông \(ANL\) ta có \(\begin{array}{l}\sin \angle ANL = \frac{{AL}}{{AN}} \Rightarrow AL = AN.\sin \angle ANL = \frac{a}{2}\sin {60^0} = \frac{{a\sqrt 3 }}{4}\\\cos \angle ANL = \frac{{NL}}{{AN}} \Rightarrow NL = AN.\cos \angle ANL = \frac{a}{2}\cos {60^0} = \frac{a}{4}\end{array}\)

Ta lại có:  \(AQ = PN \Rightarrow PL = PN + NL = AQ + NL = 2a + \frac{a}{4} = \frac{{9a}}{4}\)

Áp dụng định lí Pitago trong tam giác \(ALP\) ta có:

\(A{P^2} = A{L^2} + P{L^2} = \frac{{3{a^2}}}{{16}} + \frac{{81{a^2}}}{{16}} = \frac{{21{a^2}}}{4} \Rightarrow AP = \frac{{a\sqrt {21} }}{2}\)

Vậy \(\left| {\frac{1}{2}\overrightarrow {AB}  + 2\overrightarrow {AC} } \right| = AP = \frac{{a\sqrt {21} }}{2}.\)

Chọn  B.