Câu hỏi
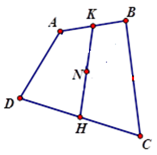
Cho tứ giác \(ABCD\). Xác định điểm \(N\) sao cho \(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow 0 \)
- A N là trung điểm của KH, K, H lần lượt là trung điểm của AC, BD.
- B N là trung điểm của KH, K, H lần lượt là trọng tâm tam giác ABC, BCD.
- C N là trung điểm của KH, K, H lần lượt là trung điểm của AD, BC.
- D N là trung điểm của KH, K, H lần lượt là trung điểm của AB, CD.
Phương pháp giải:
Áp dụng quy tắc trung điểm.
Lời giải chi tiết:
Gọi K, H lần lượt là trung điểm của AB, CD ta có
\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow 0 \Leftrightarrow 2\overrightarrow {NK} + 2\overrightarrow {NH} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {NK} + \overrightarrow {NH} = \overrightarrow 0 \Leftrightarrow N\) là trung điểm của \(KH.\)
Chọn D.