Câu hỏi
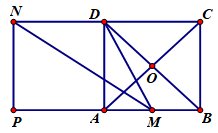
Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). Gọi \(M\)là trung điểm của \(AB\), \(N\) là điểm đối xứng với \(C\) qua \(D\). Hãy tính độ dài của vectơ \(\overrightarrow {MN} \).
- A \(\left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt {13} }}{2}\)
- B \(\left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 5 }}{3}\)
- C \(\left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 5 }}{2}\)
- D \(\left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 5 }}{4}\)
Phương pháp giải:
\(\left| {\overrightarrow {MN} } \right| = MN\)
Lời giải chi tiết:
Áp dụng định lý Pitago trong tam giác vuông \(MAD\) ta có
\(D{M^2} = A{M^2} + A{D^2} = {\left( {\frac{a}{2}} \right)^2} + {a^2} = \frac{{5{a^2}}}{4}\)\( \Rightarrow DM = \frac{{a\sqrt 5 }}{2}\)
Suy ra \(\left| {\overrightarrow {MD} } \right| = MD = \frac{{a\sqrt 5 }}{2}\).
Qua N kẻ đường thẳng song song với \(AD\) cắt\(AB\) tại \(P\).
Khi đó tứ giác \(ADNP\) là hình vuông và \(PM = PA + AM = a + \frac{a}{2} = \frac{{3a}}{2}\).
Áp dụng định lý Pitago trong tam giác vuông \(NPM\) ta có
\(M{N^2} = N{P^2} + P{M^2} = {a^2} + {\left( {\frac{{3a}}{2}} \right)^2} = \frac{{13{a^2}}}{4}\)\( \Rightarrow DM = \frac{{a\sqrt {13} }}{2}\)
Suy ra \(\left| {\overrightarrow {MN} } \right| = MN = \frac{{a\sqrt {13} }}{2}\).
Chọn A.