Câu hỏi
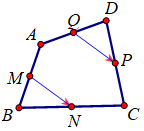
Cho tứ giác \(ABCD\). Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khăng định nào sau đây đúng
- A \(\overrightarrow {3MQ} \, = \,\overrightarrow {NP} \,\)
- B \(\overrightarrow {MQ} \, = \,\overrightarrow {NP} \,\)
- C \(\overrightarrow {2MQ} \, = \,\overrightarrow {NP} \,\)
- D \(\overrightarrow {MQ} \, = 2\,\overrightarrow {NP} \,\)
Phương pháp giải:
Tìm n bất kỳ để \(\frac{{n(n + 1)}}{2}\) chia hết cho 11
Lời giải chi tiết:
Do M, Q lần lượt là trung điểm của AB và AD nên MQ là đường trung bình của tam giác \(ABD\) suy ra \(MQ//BD\) và \(MQ = \frac{1}{2}BD\) (1).
Tương tự NP là đường trung bình của tam giác \(CBD\) suy ra \(NP//BD\) và \(NP = \frac{1}{2}BD\) (2).
Từ (1) và (2) suy ra \(MQ//NP\) và \(NP = MQ\) do đó tứ giác \(MNPQ\) là hình bình hành
Vậy ta có \(\overrightarrow {MQ} \, = \,\overrightarrow {NP} \,\).
Chọn B.
Câu hỏi trước
