Câu hỏi
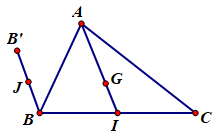
Cho tam giác \(ABC\) có trọng tâm \(G\). Gọi \(I\) là trung điểm của \(BC\). Dựng điểm \(B'\) sao cho \(\overrightarrow {B'B} = \overrightarrow {AG} \). Gọi \(J\) là trung điểm của \(BB'\). Khẳng định nào sau đây là đúng?
- A \(\overrightarrow {3BJ} = 2\overrightarrow {IG} \).
- B \(\overrightarrow {BJ} = \overrightarrow {IG} \)
- C \(\overrightarrow {BJ} = 2\overrightarrow {IG} \)
- D \(\overrightarrow {2BJ} = \overrightarrow {IG} \)
Phương pháp giải:
So sánh hướng và độ dài của \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \)
Lời giải chi tiết:
Ta có \(\overrightarrow {B'B} = \overrightarrow {AG} \) suy ra \(B'B = AG\) và \(BB'//AG\).
Do đó \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \) cùng hướng (1).
Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(IG = \frac{1}{2}AG\), \(J\) là trung điểm \(BB'\) suy ra \(BJ = \frac{1}{2}BB'\)
Vì vậy \(BJ = IG\) (2)
Từ (1) và (2) ta có \(\overrightarrow {BJ} = \overrightarrow {IG} \).
Chọn B.