Câu hỏi
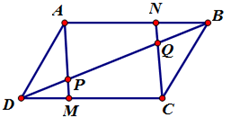
Cho hình bình hành \(ABCD\). Trên các đoạn thẳng\(DC,\,\,AB\) theo thứ tự lấy các điểm \(M,\,\,N\) sao cho \(DM = BN\). Gọi \(P\) là giao điểm của \(AM,\,\,DB\) và \(Q\) là giao điểm của \(CN,\,\,DB\). Khẳng định nào sau đây là đúng?
- A \(\overrightarrow {AM} = \overrightarrow {NC} \)
- B \(\overrightarrow {DP} = \overrightarrow {BQ} \)
- C Cả A, B đúng
- D Cả A, B sai
Phương pháp giải:
Chứng minh tứ giác \(ANCM\) là hình bình hành, \(\Delta DMP = \Delta BNQ\) (c.g.c) để so sánh độ dài các vectơ từ đó xét hướng để đưa ra kết luận.
Lời giải chi tiết:
Ta có \(DM = BN \Rightarrow AN = MC\), mặt khác \(AN\) song song với \(MC\) do đó tứ giác \(ANCM\) là hình bình hành
Suy ra \(\overrightarrow {AM} = \overrightarrow {NC} \).
Ta có: \(\angle DMP = \angle APB\) (đối đỉnh) và \(\angle APQ = \angle NQB\) (hai góc đồng vị)
\( \Rightarrow \angle DMP = \angle BNQ\,\,\,\left( { = \angle APB} \right)\).
Xét tam giác \(\Delta DMP\) và \(\Delta BNQ\) ta có:
\(\begin{array}{l}DM = NB\,\,\,\left( {gt} \right)\\\angle PDM = \angle QBN\,\,\,\left( {so\,\,le\,\,\,trong} \right)\\ \Rightarrow \Delta DMP = \Delta BNQ\,\,\,\,\left( {c - g - c} \right).\end{array}\)
\( \Rightarrow DP = QB\) (hai cạnh tương ứng).
Do đó \(\Delta DMP = \Delta BNQ\) (c.g.c) suy ra \(DP = QB\).
Dễ thấy \(\overrightarrow {DP} ,\,\,\overrightarrow {QB} \) cùng hướng vì vậy \(\overrightarrow {DP} = \overrightarrow {QB} \).
Chọn A.