Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
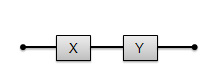
Đoạn mạch AB gồm hai hộp đen X, Y mắc nối tiếp. Trong mỗi hộp chỉ chứa một linh kiện thuộc một trong ba loại: điện trở thuần, cuộn dây hoặc tụ điện. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi 80 V và tần số f (f thay đổi được). Khi f= f0 thì điện áp hiệu dụng trên hai hộp đen lần lượt là UX = 170 V, Uy = 150 V. Sau đó bắt đầu tăng tần số f thì thấy công suất của đoạn mạch tăng. Khi f = 3f0, hệ số công suất của đoạn mạch AB xấp xỉ bằng
- A 0,142.
- B 0,149.
- C 0,187.
- D 0,203.
Phương pháp giải:
Áp dụng \(\vec{U}=\overrightarrow{{{U}_{X}}}+\overrightarrow{{{U}_{Y}}}\) mà UY2 + U2 =Ux2 \(\to \overrightarrow{{{U}_{Y}}}\bot \overrightarrow{U}\)
Sử dụng giản đồ vecto
Hệ số công suất của đoạn mạch AB bằng : \(\cos \varphi =\frac{r}{\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
Lời giải chi tiết:
Khi f= f0
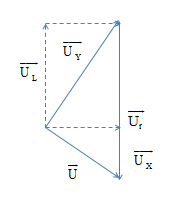
Ta có \(\vec{U}=\overrightarrow{{{U}_{X}}}+\overrightarrow{{{U}_{Y}}}\) mà UY2 + U2 =Ux2 \(\to \overrightarrow{{{U}_{Y}}}\bot \overrightarrow{U}\)
Biểu diễn các điện áp trên giản đồ vecto
Từ giản đồ, ta có X là tụ điện, Y là cuộn dây có điện trở.
\(\frac{1}{U_{r}^{2}}=\frac{1}{U_{Y}^{2}}+\frac{1}{{{U}^{2}}}\to {{U}_{r}}=\frac{1200}{17}(V)\);\({{U}_{L}}=\sqrt{U_{Y}^{2}-U_{r}^{2}}=\frac{2250}{17}(V)\)
Chuẩn hóa r=1,ta có: \(\frac{{{U}_{r}}}{{{U}_{L}}}=\frac{r}{{{Z}_{L}}}\to {{Z}_{L}}=1,875\Omega \); \(\frac{{{U}_{r}}}{{{U}_{C}}}=\frac{r}{{{Z}_{C}}}\to {{Z}_{C}}=\frac{289}{120}\Omega \)
Khi f = 3f0, \(\to Z_{L}^{'}=3.{{Z}_{L}}=5,625\Omega \); \(\to {{Z}_{C}}'=\frac{{{Z}_{C}}}{3}=\frac{289}{360}\Omega \)
Hệ số công suất của đoạn mạch AB bằng : \(\cos \varphi =\frac{r}{\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=0,203\)
Chọn D