Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng cao
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng cao
Câu hỏi
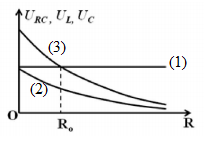
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đôi vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự gôm cuộn cảm thuân L, biên trở R và tụ điện C. Gọi URC là điện áp hiệu dụng ở hai đầu đoạn mạch gồm tụ C và biến trở R, UC là điện áp hiệu dụng ở hai đầu tụ C, UL là điện áp hiệu dụng hai đầu cuộn cảm thuần L. Hình bên là đồ thị biểu diễn sự phụ thuộc của URC, UL và UC theo giá trị của biến trở R. Khi R = 2R0, thì hệ số công suất của đoạn mạch AB xấp xỉ là
- A 0,96.
- B 0,79.
- C 0,63.
- D 0,85.
Phương pháp giải:
Phương pháp:
Sử dụng các công thức: \({{U}_{RC}}=\frac{U.\sqrt{{{R}^{2}}+Z_{C}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\), \({{U}_{C}}=\frac{U.{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\); \({{U}_{L}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
Hệ số công suất của mạch: \(\cos \varphi =\frac{R}{Z}\)
Lời giải chi tiết:
Ta có: \({{U}_{RC}}=\frac{U.\sqrt{{{R}^{2}}+Z_{C}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\), \({{U}_{C}}=\frac{U.{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\); \({{U}_{L}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
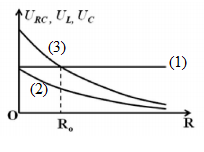
+ Khi R thay đổi, UC và UL đều chắc chắn biến thiên. Vậy đường đồ thị (1) chỉ có thể là URC. Để URC không đổi, ZL-ZC =ZC => ZL=2.ZC
Khi R=O , \({{U}_{RC}}=\frac{U.{{Z}_{C}}}{{{Z}_{L}}-{{Z}_{C}}}={{U}_{C}}\). Vậy đường đồ thị (2) biểu diễn UC, còn đường đồ thị (3) biểu diễn UL
Khi R=RO\({{U}_{RC}}={{U}_{L}}\to \frac{U.\sqrt{{{R}_{O}}^{2}+Z_{C}^{2}}}{\sqrt{{{R}_{O}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}_{O}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\to {{R}_{O}}^{2}+Z_{C}^{2}=Z_{L}^{2}\to {{R}_{O}}=\sqrt{3}.{{Z}_{C}}\)
Khi R= 2RO =\(2\sqrt{3}.{{Z}_{C}}\), hệ số công suất của đoạn mạch AB \(\cos \varphi =\frac{R}{Z}=\frac{2\sqrt{3}.{{Z}_{C}}}{\sqrt{{{(2\sqrt{3}.{{Z}_{C}})}^{2}}+Z_{C}^{2}}}=0,96\)
Chọn A