Phương pháp giải:

- Tìm tập hợp điểm biểu diễn các số phức \(z,{z_1},{z_2}\).

- Sử dụng phương pháp hình học nhận xét GTNN của \(T\).

Lời giải chi tiết:

Đặt \(z = x + yi\left( {x,y \in \mathbb{R}} \right)\) ta có:

\(\begin{array}{l}\left| {z - 1 + 2i} \right| = \left| {z + 3 - 4i} \right| \Leftrightarrow {\left| {z - 1 + 2i} \right|^2} = {\left| {z + 3 - 4i} \right|^2}\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} \Leftrightarrow 2x - 3y + 5 = 0\end{array}\)  

Do đó tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(d:2x - 3y + 5 = 0\).

Đặt \({z_1} = {a_1} + {b_1}i,{z_2} = {a_2} + {b_2}i\,\,\,\,\left( {{a_1},{b_1},{a_2},{b_2} \in \mathbb{R}} \right)\)  ta có:

\(\left| {{z_1} + 5 - 2i} \right| = 2 \Leftrightarrow {\left| {{z_1} + 5 - 2i} \right|^2} = 4 \Leftrightarrow {\left( {{a_1} + 5} \right)^2} + {\left( {{b_1} - 2} \right)^2} = 4\)  nên tập hợp điểm biểu diễn số phức \({z_1}\) là đường tròn tâm \(A\left( { - 5;2} \right)\) bán kính \(R = 2\).

\(\left| {{z_2} - 1 - 6i} \right| = 2 \Leftrightarrow {\left| {{z_2} - 1 - 6i} \right|^2} = 4 \Leftrightarrow {\left( {{a_2} - 1} \right)^2} + {\left( {{b_2} - 6} \right)^2} = 4\)  nên tập hợp điểm biểu diễn số phức \({z_2}\) là đường tròn tâm \(B\left( {1;6} \right)\) bán kính \(R = 2\).

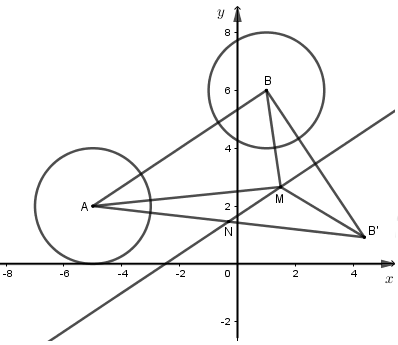
Dựng hình:

Gọi điểm \({M_1},{M_2}\) lần lượt biểu diến các số phức \({z_1},{z_2}\) thì:

\(T = \left| {z - {z_1}} \right| + \left| {z - {z_2}} \right| + 4 = M{M_1} + M{M_2} + 4 = \left( {M{M_1} + 2} \right) + \left( {M{M_2} + 2} \right) \ge MA + MB\)

Gọi \(B'\) đối xứng với \(B\) qua \(d\) thì \(MA + MB = MA + MB' \ge AB'\).

Khi đó \(T \ge MA + MB \ge AB'\).

Qua \(B\left( {1;6} \right)\) viết phương trình đường thẳng vuông góc với \(d:2x - 3y + 5 = 0\) ta được \(d':3x + 2y - 15 = 0\).

\(H = d \cap d'\) nên \(H\left( {\frac{{35}}{{13}};\frac{{45}}{{13}}} \right) \Rightarrow B'\left( {\frac{{57}}{{13}};\frac{{12}}{{13}}} \right) \Rightarrow AB' = \frac{{2\sqrt {3770} }}{{13}}\)

Chọn A.