Câu hỏi
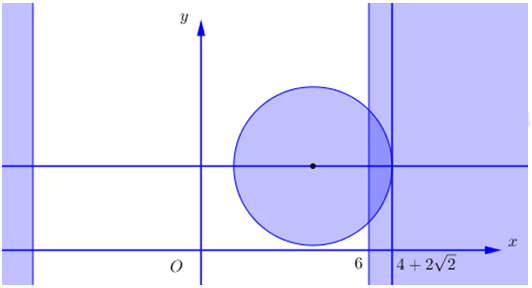
Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp các điểm biểu diễn hình học của số phức z thỏa mãn \(\left\{ \begin{array}{l}\left| {z + \overline z } \right| \ge 12\\\left| {z - 4 - 3i} \right| \le 2\sqrt 2 \end{array} \right..\) Diện tích của hình phẳng (H) là
- A \(4\pi - 4\)
- B \(8\pi - 8\)
- C \(2\pi - 4\)
- D \(8\pi - 4\)
Phương pháp giải:
+) Sử dụng phương pháp hình học.
+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Gọi \(z = x + yi \Rightarrow \overline z = x - yi\).
Theo bài ra ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\left| {z + \overline z } \right| \ge 12\\\left| {z - 4 - 3i} \right| \le 2\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {x + yi + x - yi} \right| \ge 12\\\left| {x - yi - 4 - 3i} \right| \le 2\sqrt 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left| {2x} \right| \ge 12\\\sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2}} \le 2\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 6\\x \le - 6\end{array} \right.\\{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} \le 8\end{array} \right.\end{array}\)
Diệnt tích hình (H) là diện tích phần tô đậm hơn.
Ta có \({\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 8 \Leftrightarrow y = 3 \pm \sqrt {8 - {{\left( {x - 4} \right)}^2}} \)
Vậy \(S = 2\int\limits_6^{4 + 2\sqrt 2 } {\left[ {3 + \sqrt {8 - {{\left( {x - 4} \right)}^2}} - 3} \right]dx} \approx 2,28\)
Chọn C.