Câu hỏi
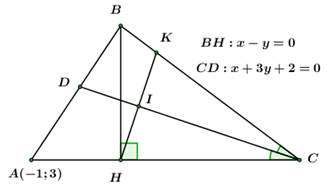
Cho \(\Delta ABC\) có \(A\left( { - 1;\,\,3} \right),\) đường cao \(BH:\,\,x - y = 0,\) phân giác trong của góc \(C\) là \(CD:\,\,x + 3y + 2 = 0.\) Tọa độ của đỉnh \(B\) là:
- A \(B\left( {4; - \,2} \right)\)
- B \(B\left( { - 3; - 3} \right)\)
- C \(B\left( {3;\,\,3} \right)\)
- D \(B\left( {4;\,\,4} \right)\)
Phương pháp giải:
Lập phương trình đường thẳng \(AC\) đi qua \(A\) và vuông góc với \(BH.\)
Từ đó ta tìm được tọa độ điểm \(C\) là giao điểm của\(AC\) và \(CD.\)
Gọi \(K\) là điểm đối xứng của \(H\) qua \(CD \Rightarrow \) tọa độ điểm \(K.\)
Lập phương trình đường thẳng \(BC\) đi qua \(K\) và \(C.\)
\( \Rightarrow B\) là giao điểm của \(BC\) và \(BH.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {{n_{BH}}} = \left( {1;\, - 1} \right).\)
Đường thẳng \(AC\) đi qua \(A\) và vuông góc với \(BH \Rightarrow AC\) nhận vecto \(\left( {1;\,\,1} \right)\) làm VTPT
\( \Rightarrow AC:\,\,x + 1 + y - 3 = 0 \Leftrightarrow x + y - 2 = 0.\)
Khi đó tọa độ điểm \(C\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + 3y + 2 = 0\\x + y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = - 2\end{array} \right. \Rightarrow C\left( {4; - 2} \right).\)
\(BH \cap AC = \left\{ H \right\} \Rightarrow \) tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + y - 2 = 0\\x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right. \Rightarrow H\left( {1;\,\,1} \right).\)
Gọi \(K\) là điểm đối xứng của \(H\) qua \(CD\)
Phương trình đường thẳng \(HK\) đi qua \(H\) và vuông góc với \(CD,\) nhận \(\left( {3; - 1} \right)\) làm VTPT là:
\(HK:\,\,\,3\left( {x - 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow 3x - y - 2 = 0\)
Gọi \(I\) là giao điểm của \(CD\) và \(HK \Rightarrow \) tọa độ điểm \(I\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + 3y + 2 = 0\\3x - y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{5}\\y = - \frac{4}{5}\end{array} \right. \Rightarrow I\left( {\frac{2}{5}; - \frac{4}{5}} \right).\)
\(K\) là điểm đối xứng của \(H\) qua \(CD \Rightarrow I\) là trung điểm của \(HK \Rightarrow K\left( { - \frac{1}{5}; - \frac{{13}}{5}} \right)\)
Phương trình đường thẳng đi qua \(C\left( {4; - 2} \right)\) và \(K\left( { - \frac{1}{5}; - \frac{{13}}{5}} \right)\) là:
\(\begin{array}{l}\frac{{x - 4}}{{ - \frac{1}{5} - 4}} = \frac{{y + 2}}{{ - \frac{{13}}{5} + 2}} \Leftrightarrow \frac{3}{5}\left( {x - 4} \right) = \frac{{21}}{5}\left( {y + 2} \right)\\ \Leftrightarrow x - 4 = 7y + 14 \Leftrightarrow x - 7y - 18 = 0\end{array}\)
Khi đó \(B\) là giao điểm của \(BH\) và \(BC \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - y = 0\\x - 7y - 18 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 3\end{array} \right. \Rightarrow B\left( { - 3; - 3} \right).\)
Chọn B.