Phương pháp giải:

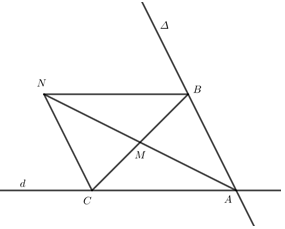
Tìm tọa độ điểm A là giao điểm của \((\Delta )\)và \((d)\)

Tìm  N  là điểm sao cho ABNC là hình bình hành

Tìm điểm B là giao của BN và \(\Delta \)

Viết phương trình đường thẳng BM  là đường thẳng cần tìm

Lời giải chi tiết:

Gọi A là giao điểm của \((\Delta )\)và \((d)\)

\( \Rightarrow \) Tọa độ điểm A  là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{{11}}\\y =  - \frac{5}{{11}}\end{array} \right. \Rightarrow A\left( {\frac{8}{{11}}; - \frac{5}{{11}}} \right).\)

Gọi \(N\left( {a;\,\,b} \right)\)   là điểm sao cho ABNC là hình bình hành

\(\begin{array}{l} \Rightarrow \overrightarrow {AM}  = \overrightarrow {MN}  \Leftrightarrow \left( {a - 1;\,b - 1} \right) = \left( {1 - \frac{8}{{11}};\,1 + \frac{5}{{11}}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 1 - \frac{8}{{11}}\\b - 1 = 1 + \frac{5}{{11}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{14}}{{11}}\\b = \frac{{27}}{{11}}\end{array} \right. \Rightarrow N\left( {\frac{{14}}{{11}};\frac{{27}}{{11}}} \right)\end{array}\)

Đường thẳng \(\left( {BN} \right)\) là đường thẳng đi qua N và song song với \((d)\)

\( \Rightarrow \left( {BN} \right):3\left( {x - \frac{{14}}{{11}}} \right) + 7\left( {y - \frac{{27}}{{11}}} \right) = 0 \Leftrightarrow 3x + 7y - 21 = 0\)

B là giao điểm của \((\Delta )\)và \((BN) \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ:\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y - 21 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{{14}}{{11}}\\y = \frac{{39}}{{11}}\end{array} \right. \Rightarrow B\left( { - \frac{{14}}{{11}};\frac{{39}}{{11}}} \right)\)

Phương trình đường thẳng \(\left( {BM} \right)\) cần tìm là: \(\frac{{x - 1}}{{ - \frac{{14}}{{11}} - 1}} = \frac{{y - 1}}{{\frac{{39}}{{11}} - 1}} \Leftrightarrow \frac{{28}}{{11}}\left( {x - 1} \right) =  - \frac{{25}}{{11}}\left( {y - 1} \right) \Leftrightarrow 28x + 25y - 53 = 0.\)

Chọn A.