1. Góc giữa hai vecto là gì?
Trong không gian, cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne \overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \). Khi đó, \(\widehat {AOB}\) \(\left( {{0^o} < \widehat {AOB} < {{180}^o}} \right)\) được gọi là góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
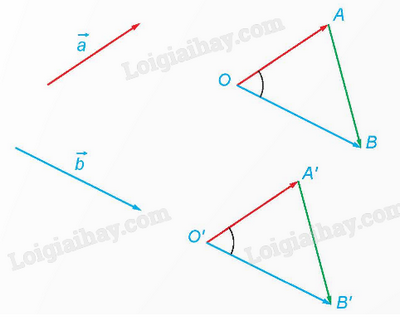
2. Công thức tính góc giữa hai vecto trong không gian
Trong không gian với hệ trục toạ độ Oxyz, cho \(\overrightarrow a \left( {{x_a};{y_a};{z_a}} \right)\) và \(\overrightarrow b \left( {{x_b};{y_b};{z_b}} \right)\).
Để tính góc \(\alpha \) giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), ta sử dụng công thức:
\(\cos \alpha = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}}}{{\sqrt {{x_a}^2 + {y_a}^2 + {z_a}^2} .\sqrt {{x_b}^2 + {y_b}^2 + {z_b}^2} }}\).
Lưu ý: \({0^o} < \alpha < {180^o}\).
Ví dụ minh hoạ:
1) Trong không gian Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(2;-1;1). Tính góc giữa hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
Giải:
Tính vecto: \(\overrightarrow {AB} = ( - 1;1;0)\), \(\overrightarrow {CD} = (2; - 1;0)\).
Tích vô hướng: \(\overrightarrow {AB} \cdot \overrightarrow {CD} = - 1 \cdot 2 + 1 \cdot ( - 1) = - 2 - 1 = - 3\).
Độ dài của các vecto: \(\left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 1)}^2} + {1^2} + {0^2}} = \sqrt 2 \), \(\left| {\overrightarrow {CD} } \right| = \sqrt {{2^2} + {{( - 1)}^2} + {0^2}} = \sqrt 5 \).
Góc giữa hai vecto: \(\cos \theta = \frac{{ - 3}}{{\sqrt 2 \cdot \sqrt 5 }} = \frac{{ - 3}}{{\sqrt {10} }} \Rightarrow \theta \approx {\rm{16}}{{\rm{2}}^o}\).
2) Cho hai vecto \(\vec a= \left( {2;1; - 2} \right)\) và \(\vec b= \left( {0;2m; - 4} \right)\). Tìm giá trị của tham số m để hai vecto \(\vec a\) và \(\vec b\) vuông góc với nhau.
Giải:
\(\vec a\bot \vec b\Leftrightarrow \vec a.\vec b= 0 \Leftrightarrow 2.0 + 1.2m + \left( { - 2} \right).\left( { - 4} \right) = 0 \Leftrightarrow m = - 4\).

 Hệ trục tọa độ trong không gian - Từ điển môn Toán 12
Hệ trục tọa độ trong không gian - Từ điển môn Toán 12 






Danh sách bình luận