Hệ trục tọa độ trong không gian - Từ điển môn Toán 12 
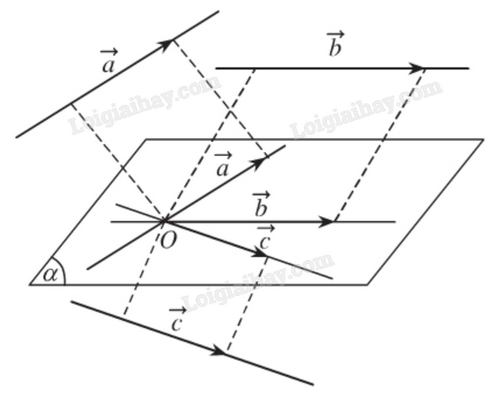
1. Vecto đồng phẳng là gì?
Vecto được gọi là đồng phẳng nếu trong không gian các giá của chúng song song với cùng một mặt phẳng.
2. Cách tìm m để ba vecto đồng phẳng bằng phương pháp toạ độ
Trong không gian với hệ trục toạ độ Oxyz, cho ba vecto \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \).
Để ba vecto trên đồng phẳng thì \(\left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c = 0\).
Ví dụ minh hoạ:
1) Cho ba vecto \(\overrightarrow a (2;5;7)\), \(\overrightarrow b (1;1; - 1)\) và \(\overrightarrow c (1;2;m)\). Tìm m để \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) đồng phẳng.
Giải:
Để \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) đồng phẳng thì \(\left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c = 0\).
Ta có \(\left[ {\overrightarrow a ,\overrightarrow b } \right] = ( - 12;9; - 3)\); \(\left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c = 0 \Leftrightarrow - 12.1 + 9.2 - 3m = 0 \Leftrightarrow m = 2\).
2) Cho ba vecto \(\overrightarrow u (2; - 1;1)\), \(\overrightarrow v (m;3; - 1)\) và \(\overrightarrow w (1;2;1)\). Tìm m để \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) đồng phẳng.
Giải:
Để \(\overrightarrow u \), \(\overrightarrow v \) và \(\overrightarrow w \) đồng phẳng thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow w = 0\).
\(\left[ {\overrightarrow u ,\overrightarrow v } \right] = ( - 2;m + 2;m + 6)\); \(\left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow w = 0 \Leftrightarrow 3m + 8 = 0 \Leftrightarrow m = - \frac{8}{3}\).
