Khoảng tứ phân vị của mẫu số liệu ghép nhóm là gì? Khái niệm, công thức và ý nghĩa - Toán 12

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm: \({\Delta _Q} = {Q_3} - {Q_1}\).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia.

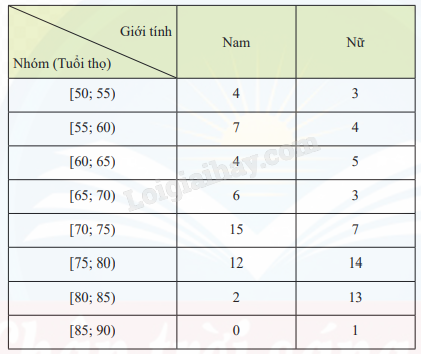
a) Hãy tính các khoảng tứ phân vị của tuổi thọ trung bình của nam giới và nữ giới trong mẫu số liệu ghép nhóm trên.
b) Hãy cho biết tuổi thọ trung bình của nam giới hay nữ giới trong mẫu số liệu ghép nhóm trên đồng đều hơn.

Giải:

Cỡ mẫu \(n = 50\).

Gọi \({x_1};{x_2}; \ldots ;{x_{50}}\) là mẫu số liệu gốc về tuổi thọ trung bình của nam giới ở 50 quốc gia được xếp theo thứ tự không giảm.

Ta có: \({x_1};{x_2}; \ldots ;{x_4} \in [50;55)\); \({x_5}; \ldots ;{x_{11}} \in [55;60)\);\({x_{12}}; \ldots ;{x_{15}} \in [60;65)\);\({x_{16}}; \ldots ;{x_{21}} \in [65;70)\);\({x_{22}}; \ldots ;{x_{36}} \in [70;75)\);\({x_{37}}; \ldots ;{x_{48}} \in [75;80)\);\({x_{49}};{x_{50}} \in [80;85)\).

Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{13}} \in [60;65)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 60 + \frac{{\frac{{50}}{4} - (4 + 7)}}{4}(65 - 60) = 61,875\).

Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{38}} \in [75;80)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 75 + \frac{{\frac{{3.50}}{4} - (4 + 7 + 4 + 6 + 15)}}{{12}}(80 - 75) = 75,625\).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 13,75\).

Gọi \({y_1};{y_2}; \ldots ;{y_{50}}\) là mẫu số liệu gốc về tuổi thọ trung bình của nữ giới ở 50 quốc gia được xếp theo thứ tự không giảm.

Ta có: \({y_1};...;{y_3} \in [50;55)\); \({y_4}; \ldots ;{y_7} \in [55;60)\);\({y_8}; \ldots ;{y_{12}} \in [60;65)\);\({y_{13}};...;{y_{15}} \in [65;70)\);\({y_{16}}; \ldots ;{y_{22}} \in [70;75)\);\({y_{23}}; \ldots ;{y_{36}} \in [75;80)\);\({y_{37}};...;{y_{49}} \in [80;85)\);\({y_{50}} \in [85;90)\).

Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_{13}} \in [65;70)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 65 + \frac{{\frac{{50}}{4} - (3 + 4 + 5)}}{3}(70 - 65) = \frac{{395}}{6}\).

Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{38}} \in [80;85)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 80 + \frac{{\frac{{3.50}}{4} - (3 + 4 + 5 + 3 + 7 + 14)}}{{13}}(85 - 80) = \frac{{2095}}{{26}}\).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{575}}{{39}}\).

b) Có \({\Delta _Q}' > {\Delta _Q}\) nên độ tuổi trung bình của nam giới đồng đều hơn.