Cách tính phương sai, độ lệch chuẩn và đo độ rủi ro với mẫu số liệu ghép nhóm - Toán 12

Xét mẫu số liệu ghép nhóm cho bởi bảng sau:

* Phương sai:

- Công thức 1: \({S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\).

- Công thức 2: \({S^2} = \frac{1}{n}\left( {{n_1}{c_1}^2 + {n_2}{c_2}^2 + ... + {n_k}{c_k}^2} \right) - {\overline x ^2}\).

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu; \(\overline x  = \frac{1}{n}\left( {{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}} \right)\) là số trung bình.

* Độ lệch chuẩn: \(S = \sqrt {{S^2}} \).

- Phương sai (độ lệch chuẩn) của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho phương sai (độ lệch chuẩn) của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu. Phương sai và độ lệch chuẩn càng lớn thì dữ liệu càng phân tán.

- Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.

Mẫu số liệu nào có phương sai và độ lệch chuẩn lớn hơn thì có độ rủi ro cao hơn.

1) Lợi nhuận của 20 nhà đầu tư quy mô nhỏ ở hai lĩnh vực A và B được cho như sau (lợi nhuận âm được hiểu là lỗ vốn):

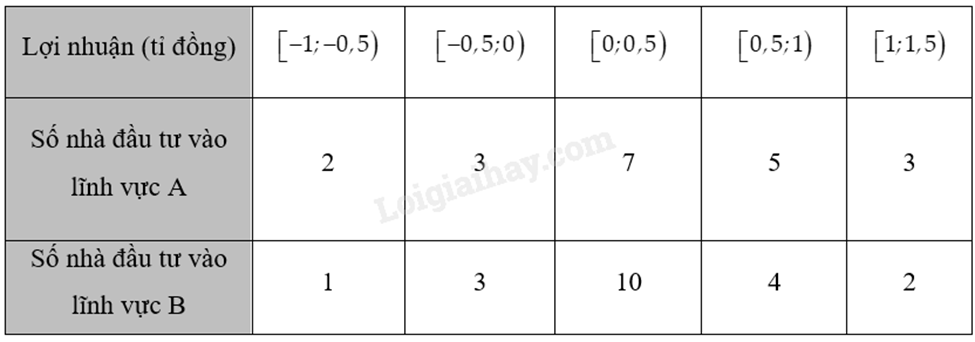
Hỏi đầu tư vào lĩnh vực nào “rủi ro” hơn?

Giải:

Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

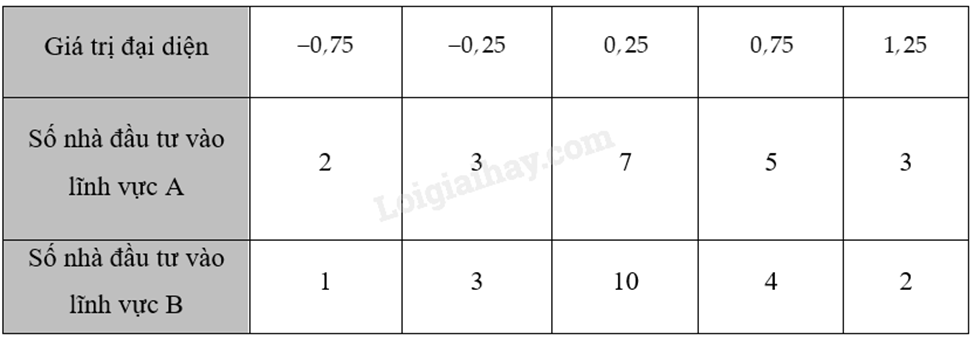
+ Xét mẫu số liệu lợi nhuận của lĩnh vực A:

Cỡ mẫu là \(n = 1 + 3 + 10 + 4 + 2 = 20\).

 Lợi nhuận trung bình của mỗi nhà đầu tư là:

\(\bar x= \frac{1}{{20}}\left[ {2 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 7 \cdot 0,25 + 5 \cdot 0,75 + 3 \cdot 1,25} \right] = \frac{7}{{20}} = 0,35\).

Độ lệch chuẩn là:

\({s_A} = \sqrt {\frac{1}{{20}}\left[ {2 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 7 \cdot 0,{{25}^2} + 5 \cdot 0,{{75}^2} + 3 \cdot 1,{{25}^2}} \right] - 0,{{35}^2}} = \frac{{\sqrt {34} }}{{10}} \approx 0,58\).

+ Xét mẫu số liệu lợi nhuận của lĩnh vực B:

Cỡ mẫu là \(n = 2 + 3 + 7 + 5 + 3 = 20\).

 Lợi nhuận trung bình của mỗi nhà đầu tư là:

\(\bar x= \frac{1}{{20}}\left[ {1 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 10 \cdot 0,25 + 4 \cdot 0,75 + 2 \cdot 1,25} \right] = \frac{{13}}{{40}} = 0,325\).

Độ lệch chuẩn là:

\({s_B} = \sqrt {\frac{1}{{20}}\left[ {1 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 10 \cdot 0,{{25}^2} + 4 \cdot 0,{{75}^2} + 2 \cdot 1,{{25}^2}} \right] - 0,{{325}^2}} = \frac{{\sqrt 5 }}{{20}} \approx 0,11\).

Suy ra \({s_A} > {s_B}\). Vậy đầu tư vào lĩnh vực A “rủi ro” hơn lĩnh vực B.

2) Một nhóm học sinh áp dụng hai thiết bị để đo công suất của một chiếc quạt điện và thu được bảng tần số ghép nhóm sau:

a) Tìm độ lệch chuẩn cho hai mẫu số liệu ghép nhóm về công suất của chiếc quạt điện khi đo theo hai phương pháp trên.

b) Từ kết quả tính được hãy cho biết thiết bị nào có kết quả đo ổn định hơn.

Giải:

a) Chọn giá trị đại diện cho mỗi nhóm, ta có bảng số liệu:

Với mẫu số liệu về kết quả đo dùng thiết bị 1:

Cỡ mẫu là \(n = 1 + 3 + 8 + 5 + 3 = 20\).

Số trung bình là \(\bar x= \frac{1}{{20}}\left( {1 \cdot 72,5 + ... + 3 \cdot 76,5} \right) = 74,8\).

Độ lệch chuẩn là \({s_1} = \sqrt {\frac{1}{{20}}\left( {72,{5^2} + ... + 3 \cdot 76,{5^2}} \right) - 74,{8^2}} \approx 1,05\).

Với mẫu số liệu về kết quả đo dùng thiết bị 1:

Cỡ mẫu là \(n = 3 + 4 + 6 + 5 + 2 = 20\).

Số trung bình là \(\bar y= \frac{1}{{20}}\left( {3 \cdot 72,5 + ... + 2 \cdot 76,5} \right) = 74,45\).

Độ lệch chuẩn là \({s_2} = \sqrt {\frac{1}{{20}}\left( {3 \cdot 72,{5^2} + ... + 2 \cdot 76,{5^2}} \right) - 74,{{45}^2}} \approx 1,2\).

b) Do \({s_1} < {s_2}\) nên thiết bị 1 cho kết quả ổn định hơn.