Cách tính độ dài đoạn thẳng bằng cách sử dụng tính chất đường trung bình - Toán 8

Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.

Chú ý:

+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

+ Mỗi tam giác có ba đường trung bình.

Ví dụ: Xét \(\Delta ABC\) có D là trung điểm của cạnh AB; E là trung điểm của cạnh AC, F là trung điểm của cạnh BC.

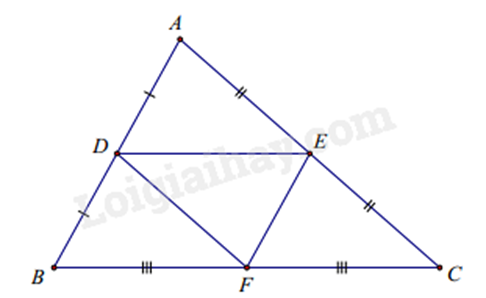
Ta có: DE, EF, DF là đường trung bình của tam giác ABC.

Để tính độ dài đoạn thẳng, ta sử dụng các tính chất đường trung bình của tam giác.

Ví dụ: Cho tam giác ABC có D là trung điểm của AB, E là trung điểm của AC và BC = 8 cm. Tính DE.

Xét tam giác ABC có D là trung điểm của AB, E là trung điểm của AC nên DE là đường trung bình của tam giác ABC.

Do đó DE = \(\frac{1}{2}\). BC = \(\frac{1}{2}\). 8 = 4 (cm).

Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.

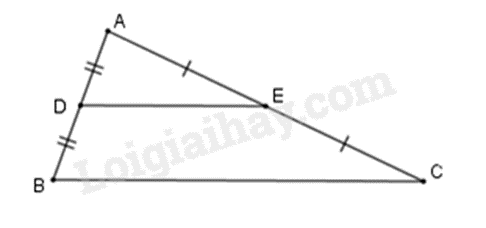
Ví dụ: \(\Delta ABC\) có \(D\) là trung điểm của AB , \(E\) là trung điểm của AC nên DE là đường trung bình của tam giác ABC thì \(DE{\rm{//}}BC;DE = \frac{1}{2}BC.\) 

Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.

Ví dụ: Cho hình vẽ, biết DF // AC. Chứng minh DF là đường trung bình của \(\Delta ABC\).

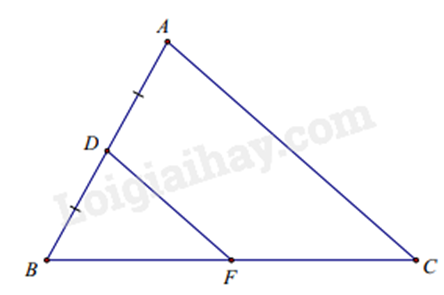
Xét \(\Delta ABC\) có AD = DB và DF // AC nên BF = FC.

Do đó DF là đường trung bình của \(\Delta ABC\).