Cách tính độ dài đoạn thẳng và tỉ số của hai đoạn thẳng bằng cách sử dụng tính chất của đường phân giác - Toán 8

Đường phân giác của một tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến cạnh đối diện, chia góc tại đỉnh đó thành hai góc bằng nhau.

Để tính độ dài đoạn thẳng và tỉ số của hai đoạn thẳng bằng cách sử dụng tính chất đường phân giác ta làm như sau:

- Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ.

- Bước 2: Sử dụng các đoạn thẳng tỉ lệ đó cùng với tính chất của tỉ lệ thức để tính độ dài đoạn thẳng chưa biết hoặc tính tỉ số đoạn thẳng.

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Ví dụ: Cho \(\Delta ABC\) có AD là đường phân giác (\(D \in BC\)). Biết AB = 4 cm, AC = 6 cm, BC = 8 cm. Tính độ dài BD, DC.

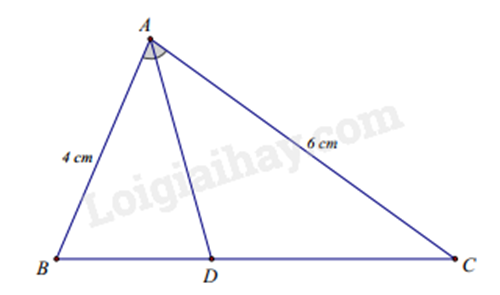
Xét \(\Delta ABC\) có AD là đường phân giác nên \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\) hay \(\frac{{DB}}{4} = \frac{{DC}}{6}\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{{DB}}{4} = \frac{{DC}}{6} = \frac{{DB + DC}}{{4 + 6}} = \frac{{BC}}{{10}} = \frac{8}{{10}} = \frac{4}{5}\)

Suy ra \(\frac{{DB}}{4} = \frac{4}{5}\) nên \(DB = \frac{{4.4}}{5} = 3,2\left( {cm} \right)\)

           \(\frac{{DC}}{6} = \frac{4}{5}\) nên \(DC = \frac{{4.6}}{5} = 4,8\left( {cm} \right)\)

Trong tam giác, đường phân giác ngoài của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Ví dụ:

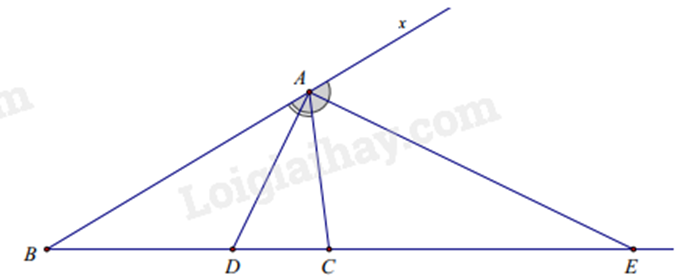
\(\widehat {xAC}\) là góc ngoài của \(\Delta ABC\) và AE là tia phân giác của \(\widehat {CAE}\).

Do đó AE là phân giác ngoài của tam giác ABC, do đó:

\(\frac{{EC}}{{AC}} = \frac{{EB}}{{AB}}\) hay \(\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}\).

Ta có AD là phân giác trong của tam giác ABC, do đó:

\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\) hay \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).

Do đó ta có tỉ lệ: \(\frac{{EB}}{{EC}} = \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).

Giả sử tất cả các biểu thức đều có nghĩa, nếu \(\frac{a}{b} = \frac{c}{d}\) thì:

+) ad = bc.

+) \(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}\).

+) \(\frac{{a + b}}{b} = \frac{{c + d}}{d}\); \(\frac{{a - b}}{d} = \frac{{c - d}}{d}\).

+) \(\frac{a}{c} = \frac{b}{d}\).