Cấu tạo nguyên tử - Từ điển Hoá 10

Cách làm các dạng bài tính nguyên tử khối trung bình - Hoá 10

1. Nguyên tử khối trung bình

Hầu hết các nguyên tố trong tự nhiên là hỗn hợp của nhiều đồng vị, mỗi đồng vị có khối lượng và tỉ lệ phần trăm số nguyên tử xác định. Nguyên tử khối của một nguyên tố là nguyên tử khối trung bình (kí hiệu là \(\mathop {\rm{A}}\limits^{\_\_} \) ) của hỗn hợp các đồng vị nguyên tố đó.

Ví dụ : bằng phương pháp phổ khối lượng , người ta xác định được trong tự nhiên nguyên tố chlorine có hai đồng vị bền là \({}_{{\rm{17}}}^{{\rm{35}}}{\rm{Cl(75,77\% ), }}{}_{{\rm{17}}}^{{\rm{37}}}{\rm{Cl(24,23\% )}}\) số nguyên tử.

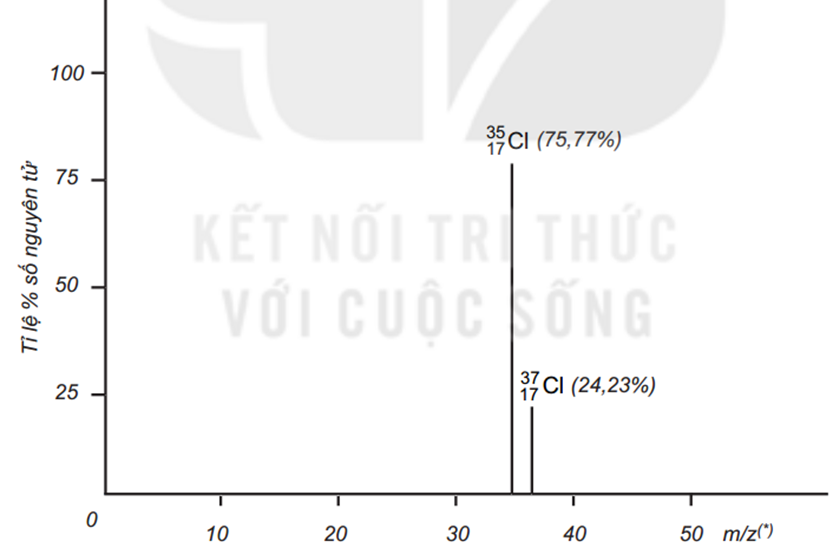
Phổ khối lượng của chlorine

Nguyên tử khối trung bình của chlorine

\(\mathop {{{\rm{A}}_{{\rm{Cl}}}}}\limits^{{\rm{\_\_}}\,\,\,\,\,\,\,} {\rm{ = }}\frac{{{\rm{35}}{\rm{.75,77 + 37}}{\rm{.24,23}}}}{{{\rm{100}}}} = 35,48 \approx 35,5\)

* Tổng quát: \({}_Z^{{A_1}}{{\rm{X}}_1}{\rm{(}}{{\rm{x}}_1}{\rm{\% ), }}{}_Z^{{A_2}}{{\rm{X}}_2}{\rm{(}}{{\rm{x}}_2}{\rm{\% )}}.....{}_Z^{{A_n}}{{\rm{X}}_n}{\rm{(}}{{\rm{x}}_n}{\rm{\% )}}\)

Ta có: \(\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} {\rm{ = }}\frac{{{{\rm{A}}_1}{\rm{.}}{{\rm{x}}_1}{\rm{ + }}{{\rm{A}}_2}{\rm{.}}{{\rm{x}}_2} + .... + {{\rm{A}}_n}{\rm{.}}{{\rm{x}}_n}}}{{{\rm{100}}}}\)

Nguyên tử khối của các nguyên tố hoá ghi trong bảng tuần hoàn là nguyên tử khối trung bình của các đồng vị trong tự nhiên.

2. Cách làm dạng bài tính nguyên tử khối trung bình từ các đồng vị

- Một số lưu ý : khí Chlorine (Cl₂); khí Oxygen (O₂), khí Nitrogen (N₂),...khí Argon (Ar), khí neon (Ne)......

- Khi đề bài cho biết số khối và % mỗi đồng vị chiếm: \({}_Z^{{A_1}}{{\rm{X}}_1}{\rm{(}}{{\rm{x}}_1}{\rm{\% ), }}{}_Z^{{A_2}}{{\rm{X}}_2}{\rm{(}}{{\rm{x}}_2}{\rm{\% )}}.....{}_Z^{{A_n}}{{\rm{X}}_n}{\rm{(}}{{\rm{x}}_n}{\rm{\% )}}\)

\(\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} {\rm{ = }}\frac{{{{\rm{A}}_1}{\rm{.}}{{\rm{x}}_1}{\rm{ + }}{{\rm{A}}_2}{\rm{.}}{{\rm{x}}_2} + .... + {{\rm{A}}_n}{\rm{.}}{{\rm{x}}_n}}}{{{\rm{100}}}}\)

- Khi đề bài cho biết số khối và tỉ lệ % số nguyên tử đồng vị \({}_Z^{{A_1}}{{\rm{X}}_1}{\rm{, }}{}_Z^{{A_2}}{{\rm{X}}_2}\) là \(\frac{{\rm{a}}}{{\rm{b}}}\)

\(\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} {\rm{ = }}\frac{{{{\rm{A}}_{\rm{1}}}{\rm{.a + }}{{\rm{A}}_{\rm{2}}}{\rm{.b}}}}{{{\rm{a + b}}}}\)

3. Cách làm dạng bài tính thành phần % số nguyên tử , khi biết số khối và nguyên tử khối trung bình

- Nguyên tử X có 2 đồng vị \({}_Z^{{A_1}}{{\rm{X}}_1}{\rm{, }}{}_Z^{{A_2}}{{\rm{X}}_2}\)có nguyên tử khối trung bình là \(\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} \). Thành phần phần trăm số nguyên tử của mỗi loại đồng vị là bao nhiêu ?

Cách 1:

a) Gọi % \({}_Z^{{A_1}}{{\rm{X}}_1}\) = a% ; %\({}_Z^{{A_2}}{{\rm{X}}_2}\)=b%

\(\left\{ \begin{array}{l}{\rm{a + b = 100}}\\{{\rm{A}}_{\rm{1}}}{\rm{.a + }}{{\rm{A}}_{\rm{2}}}{\rm{.b = 100}}{\rm{.}}\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{a = }}....\\{\rm{b = }}....\end{array} \right.\)

Vậy % \({}_Z^{{A_1}}{{\rm{X}}_1}\)= a% ; % \({}_Z^{{A_2}}{{\rm{X}}_2}\)= b%

Cách 2:

Gọi % \({}_Z^{{A_1}}{{\rm{X}}_1}\) = a% ; %\({}_Z^{{A_2}}{{\rm{X}}_2}\)=(100-a)%\(\mathop {\rm{A}}\limits^{{\rm{\_\_\_}}} {\rm{ = }}\frac{{{{\rm{A}}_{\rm{1}}}{\rm{.a + }}{{\rm{A}}_{\rm{2}}}{\rm{.(100 - a) }}}}{{{\rm{100}}}} \Leftrightarrow {\rm{a = }}.....\)

Vậy % \({}_Z^{{A_1}}{{\rm{X}}_1}\)= a% ; % \({}_Z^{{A_2}}{{\rm{X}}_2}\)= (100-a)%

4. Cách làm bài tính số lượng mỗi loại đồng vị

Nguyên tử X có 3 đồng vị:

\({}_Z^{{A_1}}{{\rm{X}}_1}{\rm{(}}{{\rm{x}}_1}{\rm{\% ) }}{}_Z^{{A_2}}{{\rm{X}}_2}{\rm{(}}{{\rm{x}}_2}{\rm{\% ) }}{}_Z^{{A_3}}{{\rm{X}}_n}{\rm{(}}{{\rm{x}}_3}{\rm{\% ) }}\)

a nguyên tử " \(a.\frac{{{x_2}}}{{{x_1}}}\) nguyên tử " \(a.\frac{{{x_3}}}{{{x_1}}}\) nguyên tử

5. Bài tập vận dụng

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE