Đề bài
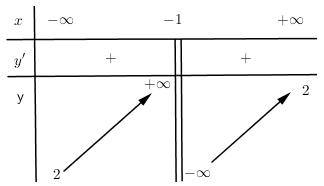
Hàm số nào dưới đây có thể có bảng biến thiên như hình vẽ?
-
A.
\(y = \dfrac{{2x - 1}}{{x - 2}}\)
-
B.
\(y = \dfrac{{2x + 3}}{{x + 1}}\)
-
C.
\(y = \dfrac{{4x - 3}}{{2x + 2}}\)
-
D.
\(y = \dfrac{{ - 2x - 5}}{{ - 1 - x}}\)
Phương pháp giải
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số và đối chiếu với các đáp án bài cho.
- Dựa và điều kiện hàm đồng biến, nghịch biến để suy ra điều kiện \(ad - bc\).
Lời giải của GV Loigiaihay.com
- Tiệm cận đứng \(x = - 1\) nên loại A.
- Tiệm cận ngang \(y = 2\), cả 3 đáp án B, C, D đều thỏa mãn.
- Hàm số đồng biến trên TXĐ nên \(ad - bc > 0\). Thử vào các đáp án chỉ có đáp án C thỏa mãn.
Đáp án : C
Chú ý
HS thường không để ý đến tính đồng biến, nghịch biến nên sẽ chọn nhầm đáp án B là sai.
Danh sách bình luận