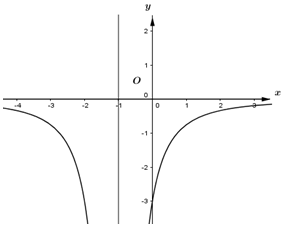
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng:
-
A.
\( - 3\)
-
B.
\( - 5\)
-
C.
\( - 2\)
-
D.
\( - 1\)
- Dựa vào dấu \(f'\left( x \right)\) xác định GTLN của hàm số \(y = f\left( x \right)\) trên \(\left[ {1;2} \right]\).
- Dựa vào TXĐ của hàm số \(y = f'\left( x \right)\) và điểm đi qua \(\left( {0; - 3} \right)\), biểu diễn 3 trong 4 ẩn \(a,\,\,b,\,\,c,\,\,d\) theo ẩn còn lại.
- Tính \(f\left( { - 2} \right)\).
Dựa vào đồ thị hàm số ta thấy \(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\), do đó \(f'\left( x \right) < 0\,\,\forall x \in \left( {1;2} \right)\).
\( \Rightarrow \) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {1;2} \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {1;2} \right]} f\left( x \right) = f\left( 2 \right)\)\( \Rightarrow \frac{{2a + b}}{{2c + d}} = 3\).
Ta có: \(f'\left( x \right) = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ { - 1} \right\} \Rightarrow \) \( - c + d = 0 \Leftrightarrow c = d\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua điểm \(\left( {0; - 3} \right)\) \( \Rightarrow \frac{{ad - bc}}{{{d^2}}} = - 3\).
\( \Rightarrow \frac{{ad - bd}}{{{d^2}}} = - 3 \Leftrightarrow a - b = - 3d = - 3c\).
Lại có \(\frac{{2a + b}}{{2c + d}} = 3 \Leftrightarrow \frac{{2a + b}}{{2c + c}} = 3\) \( \Leftrightarrow 2a + b = 9c\).
Ta có: \(\left\{ \begin{array}{l}a - b = - 3c\\2a + b = 9c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2c\\b = 5c\end{array} \right.\)\( \Rightarrow y = \frac{{2cx + 5c}}{{cx + c}}\).
Vậy \(y\left( { - 2} \right) = \frac{{ - 4c + 5c}}{{ - 2c + c}} = - 1\).
Đáp án : D
Các bài tập cùng chuyên đề
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Hàm số nào dưới đây không có cực trị?
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) với \(ad - bc \ne 0\) là:
Cho hàm số \(y = \dfrac{{x - 3}}{{2x - 6}}\), chọn kết luận đúng:
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
Giao điểm hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là:
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị như hình bên thì:
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ thì:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
Hàm số nào dưới đây có thể có bảng biến thiên như hình vẽ?
Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
Chọn kết luận đúng:
Cho hàm số \(y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).\) Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Cho hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
