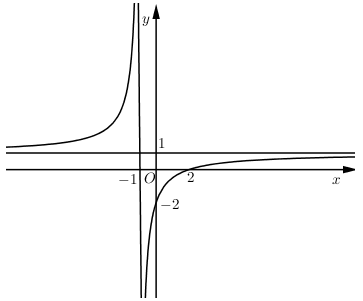
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
-
A.
\(y = \dfrac{{x - 2}}{{x + 1}}\)
-
B.
\(y = \dfrac{{x + 2}}{{x + 1}}\)
-
C.
\(y = \dfrac{{x - 2}}{{x - 1}}\)
-
D.
\(y = \dfrac{{x + 2}}{{x - 2}}\)
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm các điểm đi qua.
Đồ thị hàm số có tiệm cận ngang là $y = 1$ và tiệm cận đứng là \(x = - 1\).
Đồ thị hàm số đi qua 2 điểm \(\left( {2;\,0} \right)\) và \(\left( {0;\, - 2} \right)\).
Đáp án C và D không có tiệm cận đứng là \(x = - 1\).
Vậy loại đáp án C và D.
Xét đáp án A và B đều có tiệm cận đứng là \(x = - 1\) và tiệm cận ngang là $y = 1$.
Vì đồ thị hàm số đi qua điểm \(\left( {2;\,0} \right)\).
Thay $x = 2, y = 0$ vào hàm số thì chỉ có đáp án A thỏa mãn.
Đáp án : A
Sau khi loại trừ còn hai đáp án A, B thì có thể dựa vào tính đồng biến của hàm số để tính $ad-bc$ ở mỗi đáp án A, B rồi chọn đáp án có $ad-bc>0$
