Đề bài
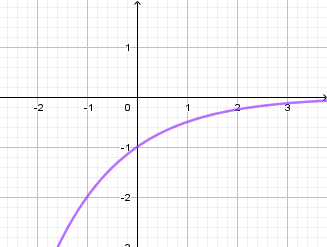
Đồ thị hàm số dưới đây là của hàm số nào?
-
A.
\(y = {2^{ - x}}\)
-
B.
\(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\)
-
C.
\(y = - {\left( {\dfrac{1}{2}} \right)^x}\)
-
D.
\(y = - {2^x}\)
Phương pháp giải
Quan sát đồ thị hàm số và nhận xét.
Lời giải của GV Loigiaihay.com
Quan sát đồ thị ta thấy nó nằm hoàn toàn phía dưới trục hoành nên loại A và B.
Lại có, đồ thị hàm số đi qua điểm \(\left( { - 1; - 2} \right)\) nên thay tọa độ điểm này vào các hàm số C và D ta được đáp án C.
Đáp án : C
Chú ý
Nhiều HS sẽ chọn đáp án D vì thấy hàm số đồng biến nên nghĩ hệ số \(a > 1\) là sai.








Danh sách bình luận