Trong không gian \(Oxyz,\) cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 4t\\z = 1\end{array} \right..\) Gọi \(\Delta \) là đường thẳng đi qua điểm \(A\left( {1;\;1;\;1} \right)\) và có vecto chỉ phương \(\overrightarrow u = \left( { - 2;\;1;\;2} \right).\) Đường phân giác của góc nhọn tạo bởi đường thẳng \(d\) và \(\Delta \) có phương trình là:
-
A.
\(\left\{ \begin{array}{l}x = 1 + 27t\\y = 1 + t\\z = 1 + t\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = - 18 + 19t\\y = - 6 + 7t\\z = 11 - 10t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 18 + 19t\\y = - 6 + 7t\\z = - 11 - 10t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = 1 - t\\y = 1 + 17t\\z = 1 + 10t\end{array} \right.\)
+) Tìm giao điểm \(I\) của \(d\) và \(\Delta .\)
+) Lấy điểm \(B\left( {{x_0};\;{y_0};\;{z_0}} \right) \in d.\)
+) Tìm tọa độ điểm \(C \in \Delta \) sao cho \(IB = IC.\)
+) Khi đó đường phân giác của \(d\) và \(\Delta \) là đường thẳng có VTCP \(\overrightarrow n = \overrightarrow {IB} + \overrightarrow {IC} \) và đi qua \(A.\)
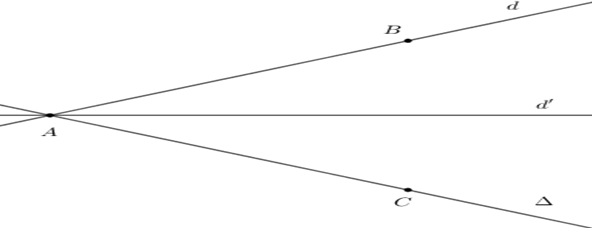
Ta có: \(\overrightarrow {{u_d}} = \left( {3;\;4;\;0} \right)\) và \(d\) đi qua \(A\left( {1;\;1;\;1} \right).\)
\( \Rightarrow d \cap \Delta = A\left( {1;\;1;\;1} \right).\)
Phương trình đường thẳng \(\Delta :\;\;\left\{ \begin{array}{l}x = 1 - 2t\\y = 1 + t\\z = 1 + 2t\end{array} \right..\)
Chọn \(B\left( {4;\;5;\;1} \right)\) là một điểm thuộc đường thẳng \(d.\)
Ta có: \(\overrightarrow {AB} = \left( {3;\;4;\;0} \right) \Rightarrow AB = 5.\)
Lấy điểm \(C\left( {1 - 2t;\;1 + t;\;1 + 2t} \right) \in \Delta \) sao cho \(AB = AC.\)
\( \Rightarrow {\left( { - 2t} \right)^2} + {t^2} + {\left( {2t} \right)^2} = 25 \Leftrightarrow {t^2} = \dfrac{{25}}{9} \Leftrightarrow t = \pm \dfrac{5}{3}.\)
+) Với \(t = \dfrac{5}{3} \Rightarrow C\left( { - \dfrac{7}{3};\;\dfrac{8}{3};\;\dfrac{{13}}{3}} \right) \Rightarrow \overrightarrow {AC} = \left( { - \dfrac{{10}}{3};\;\dfrac{5}{3};\;\dfrac{{10}}{3}} \right).\)
Khi đó ta có: \(\cos \left( {d,\;\Delta } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \dfrac{{ - \dfrac{{10}}{3}}}{{5.5}} = - \dfrac{2}{{15}} < 0 \Rightarrow \angle \left( {d;\;\Delta } \right)\) là góc tù.
+) Với \(t = - \dfrac{5}{3} \Rightarrow C\left( {\dfrac{{13}}{3}; - \dfrac{2}{3}; - \dfrac{7}{3}} \right) \Rightarrow \overrightarrow {AC} = \left( {\dfrac{{10}}{3}; - \dfrac{5}{3}; - \dfrac{{10}}{3}} \right).\)
Khi đó ta có: \(\cos \left( {d,\;\Delta } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \dfrac{{\dfrac{{10}}{3}}}{{5.5}} = \dfrac{2}{{15}} > 0 \Rightarrow \angle \left( {d;\;\Delta } \right)\) là góc nhọn nên ta cần lập phương trình đường phân giác trong TH này.
Ta có VTCP của đường phân giác của góc tạo bởi \(d\) và \(\Delta \) là: \(\overrightarrow u = \overrightarrow {AB} + \overrightarrow {AC} = \left( {\dfrac{{19}}{3};\;\dfrac{7}{3};\; - \dfrac{{10}}{3}} \right) = \dfrac{1}{3}\left( {19;\;7;\; - 10} \right).\)
Khi đó phương trình đường phân giác \(d'\) đi qua \(A\left( {1;\;1;\;1} \right)\) và có VTCP \(\overrightarrow u = \left( {19;\;7; - 10} \right)\) là: \(\left\{ \begin{array}{l}x = 1 + 19t\\y = 1 + 7t\\z = 1 - 10t\end{array} \right..\)
Với \(t = - 1\) ta có: \(I\left( { - 18; - 6;\;11} \right) \in d'.\)
Vậy đường thẳng \(d':\;\left\{ \begin{array}{l}x = - 18 + 19t\\y = - 6 + 7t\\z = 11 - 10t\end{array} \right..\)
Đáp án : B
Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho hình hộp $ABCD.A'B'C'D'$ biết $A\left( {1;0;1} \right),\,\,B\left( {2;1;2} \right),\,\,D\left( {2; - 2;2} \right)$,$A'(3;0; - 1)$, điểm M thuộc cạnh DC . GTNN của tổng các khoảng cách $AM + MC'$ là:
Trong không gian Oxyz, cho hai điểm $A(0; - 1;2),\,\,B(1;1;2)$ và đường thẳng $d:\,\,\dfrac{{x + 1}}{1} = \dfrac{y}{1} = \dfrac{{z - 1}}{1}$. Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị $T = a + 2b + 3c$ bằng
Trong không gian Oxyz, cho mặt phẳng $\left( \alpha \right):2x + y - 2z + 9 = 0$ và ba điểm $A(2;1;0),\,B(0;2;1)$, $C(1;3; - 1)$. Điểm $M \in \left( \alpha \right)$ sao cho $\left| {2\overrightarrow {MA} + 3\overrightarrow {MB} - 4\overrightarrow {MC} } \right|$ đạt giá trị nhỏ nhất. Khẳng định nào sau đây đúng?
Trong không gian Oxyz, cho đường thẳng $\Delta :\dfrac{x}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{1}$ và hai điểm $A(1;2; - 5),\,B( - 1;0;2)$. Biết điểm M thuộc $\Delta $ sao cho biểu thức $T = \left| {MA - MB} \right|$ đạt GTLN là ${T_{max}}$. Khi đó, ${T_{max}}$ bằng bao nhiêu?
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;\;0;\;2} \right)\) và đi qua điểm \(A\left( {0;\;1;\;1} \right).\) Xét các điểm \(B,\;C,\;D\) thuộc \(\left( S \right)\) sao cho \(AB,\;AC,\;AD\) đôi một vuông góc với nhau. Thể tích của khối tứ diện \(ABCD\) có giá trị lớn nhất bằng:
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):\;{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 16\) và điểm \(A\left( { - 1; - 1; - 1} \right).\) Xét các điểm \(M\) thuộc \(\left( S \right)\) sao cho đường thẳng \(AM\) tiếp xúc với \(\left( S \right),\;M\) luôn thuộc mặt phẳng có phương trình là:
Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O.\) Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = \dfrac{1}{2}MI\) (tham khảo hình vẽ). Khi đó sin của góc tạo bởi mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng:
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $M\left( {1;2;3} \right).$ Mặt phẳng $\left( P \right)$ đi qua M và cắt các tia $Ox;\,\,Oy;\,\,Oz$ lần lượt tại các điểm $A;\,\,B;\,\,C$ $\left( {A;\,\,B;\,\,C \ne O} \right)$ sao cho thể tích của tứ diện $OABC$ nhỏ nhất. Phương trình của mặt phẳng $\left( P \right)$ là
Trong hệ tọa độ Oxyz cho hai điểm \(A\left( {1;5;0} \right);\,\,B\left( {3;3;6} \right)\) và đường thẳng \(\left( d \right):\,\,\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 - t\\z = 2t\end{array} \right.\). Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng \(\sqrt a + \sqrt b \) với a, b là các số nguyên. Khi đó:
