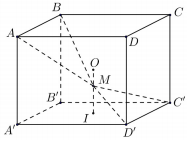
Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O.\) Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = \dfrac{1}{2}MI\) (tham khảo hình vẽ). Khi đó sin của góc tạo bởi mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng:
-
A.
\(\dfrac{{17\sqrt {13} }}{{65}}\)
-
B.
\(\dfrac{{6\sqrt {85} }}{{85}}\)
-
C.
\(\dfrac{{7\sqrt {85} }}{{85}}\)
-
D.
\(\dfrac{{6\sqrt {13} }}{{65}}\)
Sử dụng phương pháp tọa độ trong không gian để làm bài toán.
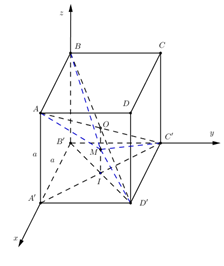
Gọi hình lập phương có cạnh là \(a.\)
Xét hệ trục tọa độ như hình vẽ ta có:
\(\begin{array}{l}B'\left( {0;\;0;\;0} \right),\;\;A'\left( {a;\;0;\;0} \right),\;C'\left( {0;\;a;\;0} \right),\;D'\left( {a;\;a;\;0} \right),\\A\left( {a;\;0;\;a} \right),\;I\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;0} \right),\;B\left( {0;\;0;\;a} \right),\;O\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{a}{2}} \right).\\ \Rightarrow \overrightarrow {OI} = \left( {0;\;0;\;\dfrac{a}{2}} \right) \Rightarrow \overrightarrow {OM} = \dfrac{1}{3}\overrightarrow {OI} = \left( {0;\;0;\;\dfrac{a}{6}} \right).\\ \Rightarrow \left\{ \begin{array}{l}{x_M} - {x_O} = 0\\{y_M} - {y_O} = 0\\{z_M} - {z_O} = \dfrac{a}{6}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{a}{2}\\{y_M} = \dfrac{a}{2}\\{z_M} = \dfrac{{2a}}{3}\end{array} \right. \Rightarrow M\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{{2a}}{3}} \right).\end{array}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {MA} = \left( {\dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MB} = \left( { - \dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MC'} = \left( { - \dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right),\;\overrightarrow {MD'} = \left( {\dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right).\\ \Rightarrow {\overrightarrow n _{\left( {MAB} \right)}} = \left[ {\overrightarrow {MA} ,\;\overrightarrow {MB} } \right] = \left( {0; - \dfrac{{{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) = - {a^2}\left( {0;\;\dfrac{1}{3};\;\dfrac{1}{2}} \right).\\{\overrightarrow n _{\left( {MC'D'} \right)}} = \left[ {\overrightarrow {MC'} ,\;\overrightarrow {MD'} } \right] = \left( {0; - \dfrac{{2{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) = - {a^2}\left( {0;\;\dfrac{2}{3};\;\dfrac{1}{2}} \right).\end{array}\)
Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {M'C'D'} \right).\)
$\begin{array}{l} \Rightarrow \cos \alpha = \dfrac{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}.{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}}{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}} \right|.\left| {{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}} = \dfrac{{\left| {\dfrac{1}{3}.\dfrac{2}{3} + \dfrac{1}{2}.\dfrac{1}{2}} \right|}}{{\sqrt {\dfrac{1}{9} + \dfrac{1}{4}} .\sqrt {\dfrac{4}{9} + \dfrac{1}{4}} }} = \dfrac{{17\sqrt {13} }}{{65}}.\\ \Rightarrow sin\alpha = \sqrt {1 - {{\cos }^2}\alpha } = \dfrac{{6\sqrt {13} }}{{65}}.\end{array}$
Đáp án : D
Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho hình hộp $ABCD.A'B'C'D'$ biết $A\left( {1;0;1} \right),\,\,B\left( {2;1;2} \right),\,\,D\left( {2; - 2;2} \right)$,$A'(3;0; - 1)$, điểm M thuộc cạnh DC . GTNN của tổng các khoảng cách $AM + MC'$ là:
Trong không gian Oxyz, cho hai điểm $A(0; - 1;2),\,\,B(1;1;2)$ và đường thẳng $d:\,\,\dfrac{{x + 1}}{1} = \dfrac{y}{1} = \dfrac{{z - 1}}{1}$. Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị $T = a + 2b + 3c$ bằng
Trong không gian Oxyz, cho mặt phẳng $\left( \alpha \right):2x + y - 2z + 9 = 0$ và ba điểm $A(2;1;0),\,B(0;2;1)$, $C(1;3; - 1)$. Điểm $M \in \left( \alpha \right)$ sao cho $\left| {2\overrightarrow {MA} + 3\overrightarrow {MB} - 4\overrightarrow {MC} } \right|$ đạt giá trị nhỏ nhất. Khẳng định nào sau đây đúng?
Trong không gian Oxyz, cho đường thẳng $\Delta :\dfrac{x}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{1}$ và hai điểm $A(1;2; - 5),\,B( - 1;0;2)$. Biết điểm M thuộc $\Delta $ sao cho biểu thức $T = \left| {MA - MB} \right|$ đạt GTLN là ${T_{max}}$. Khi đó, ${T_{max}}$ bằng bao nhiêu?
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;\;0;\;2} \right)\) và đi qua điểm \(A\left( {0;\;1;\;1} \right).\) Xét các điểm \(B,\;C,\;D\) thuộc \(\left( S \right)\) sao cho \(AB,\;AC,\;AD\) đôi một vuông góc với nhau. Thể tích của khối tứ diện \(ABCD\) có giá trị lớn nhất bằng:
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):\;{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 16\) và điểm \(A\left( { - 1; - 1; - 1} \right).\) Xét các điểm \(M\) thuộc \(\left( S \right)\) sao cho đường thẳng \(AM\) tiếp xúc với \(\left( S \right),\;M\) luôn thuộc mặt phẳng có phương trình là:
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 4t\\z = 1\end{array} \right..\) Gọi \(\Delta \) là đường thẳng đi qua điểm \(A\left( {1;\;1;\;1} \right)\) và có vecto chỉ phương \(\overrightarrow u = \left( { - 2;\;1;\;2} \right).\) Đường phân giác của góc nhọn tạo bởi đường thẳng \(d\) và \(\Delta \) có phương trình là:
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $M\left( {1;2;3} \right).$ Mặt phẳng $\left( P \right)$ đi qua M và cắt các tia $Ox;\,\,Oy;\,\,Oz$ lần lượt tại các điểm $A;\,\,B;\,\,C$ $\left( {A;\,\,B;\,\,C \ne O} \right)$ sao cho thể tích của tứ diện $OABC$ nhỏ nhất. Phương trình của mặt phẳng $\left( P \right)$ là
Trong hệ tọa độ Oxyz cho hai điểm \(A\left( {1;5;0} \right);\,\,B\left( {3;3;6} \right)\) và đường thẳng \(\left( d \right):\,\,\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 - t\\z = 2t\end{array} \right.\). Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng \(\sqrt a + \sqrt b \) với a, b là các số nguyên. Khi đó:
